Sommaire
Article d’introduction à la technique de l’interférométrie des tavelures, paru dans le n°1 de la revue Francophone des observateurs d’étoiles doubles (https://etoilesdoubles.org/)
Introduction :
Interférométrie des tavelures. Voilà dans l’imaginaire collectif de l’astronomie amateur, deux mots collés ensembles et qui laissent une impression de complexité de mise en œuvre hors de portée de l’observateur. Il s’agit pourtant d’une technique relativement simple dans sa mise en œuvre à l’aide des outils actuels de l’astronomie amateur. Mais quel est le but de final de cette technique. Les observateurs d’étoiles doubles, constatent que le pouvoir de résolution constaté de leurs instruments atteint rarement le pouvoir théorique auquel il seraient en droit de s’attendre. La limite de Rayleigh, dépendant du diamètre de l’objectif de la lunette ou d’un télescope, n’est atteinte au cours de nos observations et mesures que lors d’instants fugaces, et cela même seulement si nous avons de la chance. Souvent l’observateur déçu éteint sont installation avant d’avoir eu la possibilité de faire une mesure. En effet, l’optique d’acquisition n’est pas uniquement constituée de miroirs ou de lentille, il faut aussi considérer l’atmosphère et ses couches d’air turbulentes situées entre l’objet de nos convoitise (l’étoile) et notre système de prise de vue. Et bien l’interférométrie des tavelures est une technique simple, permettant dans le cas d’étoiles doubles ou multiples, de s’affranchir purement et simplement de la limitation imposée par l’atmosphère. C’est en deux mots, un technique de « restauration du pouvoir théorique » d’un instrument. L’interférométrie des tavelures est une idée relativement ancienne, issue principalement des travaux de A. Labeyrie (1970), et quelques pionnier, qui après avoir effectué des tentatives fructueuses en interférométrie de Fizeau-Michelson (que l’on pourrait qualifier d’interférométrie « classique »), se sont penchés sur la structure des images en pleine ouverture, et y ont constaté ce que Paul Couteau cite dans son ouvrage de référence sur le mesure des étoiles doubles « L’observation des étoiles doubles visuelles »: A. Labeyrie et ses collaborateurs (1970) atteignent le fond du problème en exploitant l’ensemble de l’image à pleine ouverture. Ils étudient d’abord la formation de l’image d’une étoile, perturbée par l’atmosphère, au foyer d’un grand télescope. La cinématographie permet une étude détaillée de la structure complexe de cette image, qui se présente sous la forme d’une grappe de raisins, dont chaque grain est animé d’une vive agitation et est d’une durée de vie très courte. Ils partent de l’idée que cette image résulte d’effets d’interférences entre le faisceau incident et les fluctuations spatiales aléatoires de phases Cette définition qui par bien des aspects peu paraître abstraite et compliquée (fluctuation spatiale aléatoire de phase n’est pas un terme très courant en astronomie amateur), cache en fait un principe d’optique que l’on néglige souvent d’aborder en astronomie optique et qui pourtant revêt un aspect fondamental : la nature ondulatoire de la lumière.
Comprendre la formation des images :
La première notion incontournable dont nous avons besoin de prendre conscience est la nature propre de la lumière, et plus particulièrement sa nature ondulatoire. Par définition la lumière est une radiation électro-magnétique, c’est a dire un rayonnement faisant intervenir un champ magnétique et un champ électrique,et dont on peut étudier les effets soit par la mécanique classique (la lumière est associée à une particule : le photon), soit par la mécanique ondulatoire (la lumière est associée à une onde). Pour expliquer ce qu’est une onde prenons l’exemple de la surface d’un liquide au repos. Si l’on laisse tomber une goutte d’eau sur cette surface, on constate que le liquide se recouvre de cercles concentriques (on peut voir ci dessous 1/4 des cercles concentriques et le centre d’excitation de la surface du liquide). Si de plus on regarde cette surface par la tranche on observe le schéma ci-dessous :
Chaque particule de lumière c’est à dire chaque photon est porteur d’une quantité d’énergie notée E et dont la valeur dépend des caractéristiques de l’onde associée à ce photon. La formule donnant l’énergie du photon est la suivante :
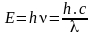
avec h est la constante de Planck, c la vitesse de la lumière dans le vide, la fréquence de l’onde [hz] et l est la longueur d’onde.
La longueur d’onde est la distance, exprimée en mètres entre deux sommets ou deux creux de cette onde. Supposons maintenant que l’on pose un bouchon à la surface du liquide et recommençons l’expérience précédente. Lorsque la surface du liquide entre en oscillation ,on constate que le bouchon n’est soumis qu’a des mouvements verticaux : il ne fait que monter ou descendre sans se déplacer par rapport à sa position d’origine. On appellera fréquence de l’onde le nombre de passage du bouchon par sa position la plus haute (ou la plus basse , ce qui revient au même) et par unité de temps. C’est en fait le nombre d’oscillation d’un point du liquide par seconde. L’amplitude de l’onde,est égale à la hauteur maximum atteinte par la bouchon lors de son déplacement verticale. Lorsque l’ on se place dans le vide ,et que l’on fait varier l’amplitude d’un champ électrique et d’un champ magnétique de la même manière que l’on a fait varier la hauteur de la surface de l’eau tout à l’heure ,on produit des photons . On peut définir le front d’onde comme étant l’ensemble des points de la surface de même hauteur, par exemple l’ensemble des « maxima » de l’onde. On peut d’ailleurs noter que la direction de propagation de l’onde défini la direction du rayon lumineux équivalent, que l’on utilise dans le cas de l’optique géométrique. La phase se défini comme l’avance ou le retard de propagation de cette onde lors de sa propagation dans l’espace, depuis l’émission par la source dans un cas idéal. En effet, sans perturbation de la vitesse de propagation du front d’onde, la phase de l’onde reste constante, et la forme du front d’onde n’est alors pas déformé par le milieu dans lequel il se propage.

On peut d’ailleurs faire une analogie simple avec la propagation de la houle à la surface de l’océan. Les vagues de houle sont parallèles et horizontales sur ce cliché (figure 2). La houle est caractérisée par sa fréquence, son amplitude, et chacune des oscillations est en phase avec la vague suivante. On peut remarquer, mais ce n’est pas le propos de cet article, que le bateau laisse dans son sillage, une vague se superposant à la houle. Apparaît alors un phénomène d’interférence entre la houle et cette vague de sillage, pour lequel les creux et bosses auront des amplitudes et de fréquences différentes. Nous en reparlerons plus tard. Pour comprendre le phénomène d’arrivée de ces vagues de champs électrique sur la pupille du télescope, plaçons nous dans le cas idéal d’une source quasi ponctuelle située loin du système d’acquisition. Une étoile peut être, en première approximation, et vu la distance à laquelle elle se situe, considérée comme une source ponctuelle. Une source ponctuelle constitue un émetteur de front d’onde circulaire. Après avoir parcouru une distance grande devant la longueur d’onde, le front d’onde incident peut être approximé comme une onde plane. Ainsi un télescope situé dans l’espace verra arriver sur son collecteur (on appelle couramment d’ailleurs l’entrée du système optique la pupille) un front d’onde plan sans erreur de phase (ou phase constante sur la pupille ce qui reviens au même) :
Comment se forme alors l’image de l’étoile au foyer du télescope ? Le principe de base pour expliquer ce que l’on va retrouver dans le plan focal, à été démontré par les premiers opticiens à avoir «senti» la nature ondulatoire de la lumière. Ces personnages scientifiquement célèbres ont postulé un principe simple, et qui explique parfaitement le phénomène de diffraction : le principe de Huygens-Fresnel. Ce principe se résume de la manière suivante : Si chaque point M (représentés en jaune sur la figure 4) de la surface de la pupille reçoit une onde d’amplitude donnée de longueur d’onde connue, le point M peut alors être considéré comme une source ponctuelle émettant à son tour une onde de même amplitude, de même longueur d’onde et en phase avec l’onde qui lui a donné naissance. Le schéma suivant illustre ce principe (source Wikipédia) :
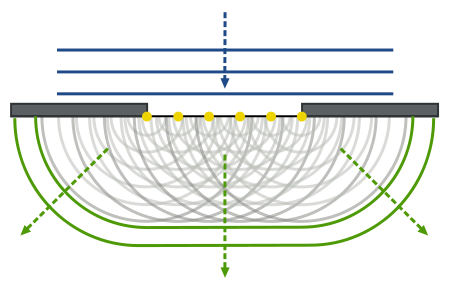
L’optique permettant ensuite de focaliser cette onde résultante, sert à courber le front d’onde de manière à ce que le front d’onde résultant produise un maximum d’intensité au niveau du plan focal. Les flèches en pointillées représentant la direction de propagation du front sur la figure 4, vont devenir convergentes après passage dans l’optique de focalisation (figure 5).
Donc en considérant deux points quelconque de la pupille, et se comportant comme le veut le principe de Huygens-Fresnel, ces points M1 et M2 vont produire chacun une onde sphérique de même fréquence, phase et de même amplitude. Chaque point source de la pupille pris deux à deux, va donc interférer dans le plan focal en produisant au point P appartenant à ce dernier plan, la somme du champs produit par M1 et du champs produit par M2. Si le point P se trouve sur l’axe, la distance parcourue par l’onde issue de M1 est la même que celle du champs parcouru par l’onde issue de M2. L’intensité résultante au point du foyer sur l’axe sera donc maximale. Comme la vague de sillage du bateau s’additionne à la houle (voir Figure 2), il existe des points du plan focal ou l’intensité du champs résultant est la somme des champs issue de M1 et de M2. Il s’agit des points pour lesquels la différences de trajets pour atteindre le point P est égal à un nombre entier multiplié par la longueur d’onde. Mais que se passe-t-il pour un point quelconque P du plan focal en dehors de l’axe ? Et bien l’onde issue de M1 aura moins de chemin à parcourir que l’onde issue de M2 (Figure 5). Cette différence de marche fait que l’onde issue de M2 sera en retard par rapport à celle issue de M1. Si le retard est exactement de la moitié de la longueur d’onde, la somme des deux ondes est nulle. La valeur de l’intensité du champs au point P sera nulle. Pour reprendre cet exemple de la houle, la somme de la vague issue de M1 et de la vague issue de M2 sera nulle, et ce si la différence de marche est égale à la moitié de la longueur d’onde. Chaque points de la pupille pris deux à deux va interférer au foyer en provoquant une variation périodique de l’intensité du champs. Si l’on isole d’ailleurs ces 2 points M1 etM2 de la pupille en utilisant un masque a 2 trous, le résultat au niveau du plan focal est une succession de franges alternativement claires et sombres, résultant de la différence de trajets entre les ondes issues de M1 et M2, atteignant le point P du plan focal. C’est la base de l’interférométrie dite « classique ».
Que se passe-t-il dès lors que l’on considère tout les couples de points appartenant à la pupille d’entrée et que l’on regarde la contribution de tous les points de la pupille ensemble ? Et bien la somme des contributions respectives de toute ces propagations d’ondes cumulées sur l’ensemble de la pupille, avec pour chacune une différence de marche particulière, amènent au final une figure unique, bien connue des astronomes amateurs : le disque (ou tache) d’Airy.

Figure 6 : la tache d’Airy
La tache d’Airy est donc la forme parfaite obtenue au foyer d’un instrument lorsqu’une source ponctuelle située à l’infini, éclaire uniformément la pupille d’un télescope ou d’une lunette. Malheureusement, et nous savons tous cela d’expérience, Ce « graal » des conditions d’observations, que nous ne pouvons avoir dans les fait que si nous sommes en dehors de l’atmosphère ou en des lieux très peu perturbés, comme au sommet de certaines montagnes, n’est atteint que de manière très fugace, lorsque l’atmosphère nous autorise un minimum de perturbations du front d’onde à l’entrée sur la pupille. Comment expliquer alors simplement ce que provoque l’atmosphère pour déformer physiquement le front d’onde et faire disparaître le disque d’Airy, au profit d’une forme totalement aléatoire ?
Dégradation des images par l’atmosphère :
La turbulence atmosphérique constitue le facteur majeur de dégradation des images astronomiques acquise au niveau du sol, qu’il s’agisse d’images faites avec des moyens professionnels ou amateurs. La couche d’air située entre nous et l’espace est turbulente, au sens ou l’indice de réfraction de l’air (c’est à dire le rapport de la vitesse de propagation dans le vide à la vitesse de propagation dans le milieu transparent) n’est pas constant sur la totalité du trajet de l’onde avant l’arrivée sur la pupille. On peut dire que la vitesse de formation de l’onde va ralentir en traversant le milieu transparent (cela est vrai dans n’importe quel matériau transparent). En supposant le matériau traversé complètement homogène, tout les rayons lumineux verraient leur propagation ralentie de manière homogène et le front d’onde resterait plan. Les inhomogénéités de pression (statique et dynamique, c’est à dire le vent), de température et de pression de vapeur d’eau vont modifier la vitesse de propagation de l’onde au cours de la traversée des couches turbulentes. La conséquence directe en est que la phase de l’onde sera modifiée, et le front d’onde à l’arrivée sur la pupille ne sera au final plus rigoureusement plan mais bosselé, comme pourrais l’être la surface de la houle sous le vent :

Figure 7 : Perturbation aléatoire du front d’onde (exemple de la houle)
La déformation du front d’onde générées par les bulles d’indice différents peuvent se comprendre mathématiquement mais sans équations, il est possible de comprendre l’effet induit sur la déformation, le « bosselage » de l’onde. Sur la figure 8, le front d’onde incident se déplace de la gauche vers la droite, et traverse des bulles d’indices (ou cellules de turbulences) différents, générées par exemple par une variation de la température rencontrée.
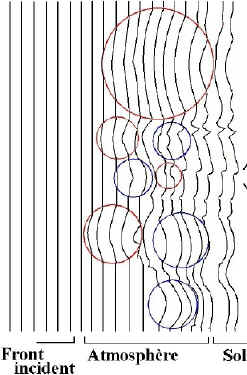
Figure 8 : Perturbation du front d’onde par variation d’indice optique
Les bases mathématiques de la décomposition spatiale de la turbulence ont été étudiées par le mathématicien russe Kolmogoroff (Kol 1941) qui a défini l’échelle minimale d’une cellule de turbulence comme suit : Dans un fluide en mouvement, l’échelle minimale d’une cellule de turbulence est donnée par la dimension de Kolmogoroff. Cette dimension ne dépend que de la viscosité du fluide (n) et de son énergie cinétique par unité de masse (e). Il en découle directement qu’a l’échelle de la cellule de Kolmogoroff, la viscosité domine et l’énergie cinétique du fluide est dissipée en chaleur. Les deux conséquences directes en sont que (et c’est ce qu’il faut en retenir) : – Plus la température locale augmente, plus les cellules sont petites, – Plus la cellule est chaude, plus elle évolue vite. Comprenant alors la dynamique du fluide atmosphérique, Tatarski (1961) effectue la transposition de la modélisation des cellules de turbulence au sens de Kolmogoroff en terme de variations des indices optiques, pour modéliser les effets de déformation du front d’onde dût à la variation de phase avant d’arriver sur la pupille du télescope. Lors de la traversée de zones plus ou moins dense (ou chaude ou froides), les points du front d’onde sont plus ou moins ralentis, ce qui affecte la forme générale du front d’onde au moment de l’arrivée sur la pupille du télescope. Toute l’analyse que l’on peut faire des effets de la turbulence résulte des caractéristiques de déformation de ce front d’onde par rapport à la pupille. La déformation totale du front d’onde à l’arrivée sur la pupille est donc la résultante de déformation par les fluctuations d’indice intégrées du sol à l’espace (Fonction de structure du front dépendant du profil de la turbulence en altitude (aussi appelée C²n(z) avec z l’altitude de la couche turbulente). Les conséquences directes de déformation du front à l’arrivée sur la pupille sont des effets de courbure à différentes échelles spatiales du front d’onde. La turbulence se décompose alors de manière assez simple en considérant la taille de l’objectif du système d’acquisition (pupille) par rapport à la dimension angulaire de la perturbation atmosphérique.
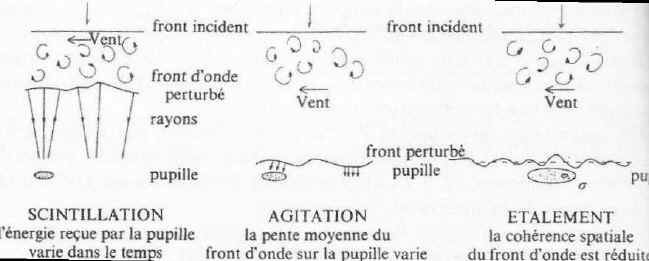
Figure 9 : les effets de déformation du front d’onde
En partant des objectifs de diamètre le plus petit, jusqu’au diamètre les plus grands, on peut décomposer la turbulence suivant les 3 phénomènes prépondérants simples suivant :
– La Scintillation (D<100mm): Il s'agit de la fluctuation de l'éclat d'une étoile, lorsqu'elle est observée avec l’œil ou une pupille de petit diamètre. La scintillation correspond à un étalement ou une concentration de l'énergie du front d'onde. En d'autre termes, la turbulence dans l'axe de visée, provoque un effet de lentille qui peut être soit convergente, soit divergente, et ce avec une variation dans le temps généralement rapide.
- L'agitation (100mm
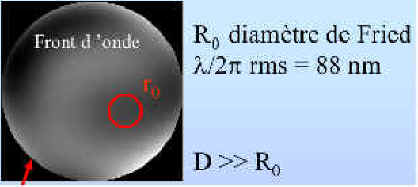
Figure 10 : Diamètre de Fried dans la pupille (crédit Cyril Cavadore)
Du point de vue de la pupille dans son ensemble, chaque sous pupille de dimension r0 va interférer avec ses voisines, et provoquer une image instantanée étalée, et constitués d’une multitude de sous figures de diffractions dont les dimensions sont celle de la tache d’Airy du télescope en pleine ouverture. Ces grappes de lumières portant le nom de tavelures (Speckles en Anglais), et ont été mis en évidence par A. Labeyrie en 1974 Deux points particuliers sont à retenir de l’effet des tavelures sur l »image d’une étoile – Le rapport du diamètre sur r0 caractérise la dégradation de la résolution donc l’étalement – On peut noter que le nombre de tavelures dans une image est (D/r0)² Plus le diamètre est important et plus les tavelures seront nombreuses pour un r0 donné. Mais ce qui est intéressant est aussi que plus le r0 est petit et plus le nombre de tavelures sera important pour un diamètre de télescope fixé. De plus, le réseau de tavelures évolue très vite, si l’on se souvient de ce que nous a appris Kolmogoroff. Cela veux donc dire que saisir les tavelures en imagerie CCD nécessite des temps de poses extrêmement courts. Typiquement les tavelures apparaissent au dessous de 10ms de poses. Si l’exposition dépasse ce que l’on appelle le « temps de cohérence » de la turbulence, les tavelures sont diluées, et l’image d’une étoile n’apparaît plus sous forme de ces « grappes de raisin » mais sous une forme plutôt patatoïde, comme on peut le voir sur la figure 13.
 |  |  |
| Image instantanée d’un point (pas de perturbation de phase) =Tache d’Airy | Image instantanée d’un point (avec perturbation de phase) =Étalement | Tavelures cumulées =Étalement |
Figure 13 : Effet de l’atmosphère et de l’accumulation des poses
Seule l’image de gauche est une image simulée (image (a)). A très court temps de pose (10ms : image (b)), on obtient une fonction d’étalement quasi-instantanée (ici obtenue au T60 du pic du midi). Si l’on dispose d’un moyen de compensation du tip/tilt (ici la compensation a été réalisée via un software, image (c)) la pose cumulée est représentative de défauts optiques du télescope (défauts statiques dans le temps), et de la dispersion du flux lumineux dût à l’intégration des fonctions d’étalements instantanées aléatoires. On obtient alors une image d’étoile (dite aussi réponse impulsionnelle du télescope), représentative de ce que Fried appelait le « seeing longue pose », et dont la valeur est directement liée à la distribution statistique du r0 pendant la pose. En conclusion sur la nature des tavelures, il s’agit donc d’une image d’interférences dans le plan focal dut à la déformation du front d’onde issus d’une étoile unique, par les perturbations atmosphérique le long de la ligne de visée. Ce phénomène n’apparaît que lors de temps d’exposition suffisamment court pour ne pas « diluer » les tavelures.
Tavelures sur étoiles doubles :
Chaque étoiles observé dans un télescope amateur, se comporte comme une source ponctuelle au regard de la dimension angulaire extrêmement faible de l’objet. Donc chaque étoile dans le champs d’un télescope va produire son propre réseau de tavelures à chaque instant. Aussi que peut-on attendre de l’image d’une étoile double dont chaque front d’onde dans le champs du télescope est perturbé par les bulles de turbulence ? Deux cas peuvent se présenter. Pour un couple d’étoile de séparation donnée, il existe une zone angulaire au sein de laquelle la perturbation de phase reste homogène. Chaque étoile produit alors le même réseau de tavelures, écarté de la séparation du couple d’étoiles. On appelle cette zone angulaire la zone d’isoplanétisme :
Figure 14 : l’Angle d’isoplanétisme
En appelant epsilon_r la séparation du couple, et théta_0 l’angle d’isoplanétisme, si théta_0 et supérieur à epsilon_r alors le réseau de tavelure produit par chaque étoile est extrêmement semblable. On voit sur les clichés suivants (Figure 15 : extraits d’une séquence vidéo à très court temps de pose), image de gauche que les deux étoiles du couples, obtenues à la lunette de 55cm de l’observatoire de Nice, présentent un réseau de tavelures extrêmement semblables, dut à une similarité des perturbations respectives de la turbulence dans la ligne de visée de chaque étoiles. A contrario, la situation est différente si les perturbations deviennent incohérentes entre les axes de visée de chacune des deux étoiles. Les réseaux de tavelures deviennent incohérent l’un par rapport a l’autre, il deviens donc difficile de séparer les étoiles du couple (image de droite). On sens malgré tout qu’il y à ici une possibilité de recherche de similarité du réseau de tavelure produit par chaque composante du couple qui permettrait de remonter à la position des deux étoiles en séparation et en angle.
 |  |
 |  |
| Images : B.Trégon, J. Sérot |
Figure 15 : Tavelures et isoplanétisme
Extraction des positions des étoiles dans les tavelures :
La méthode de récupération des positions des sources de chaque réseau de tavelures porte le doux nom d’auto-corrélation. C’est une méthode simple dans son principe, que l’on peut décrire rapidement de la manière suivante : En supposant que l’on prenne deux exemplaires de l’image que l’on positionne l’une sur l’autre en les décalant, pixels par pixels. Le produit des pixels superposés de la première image et de la deuxième sera égal à zéro tant que les réseau de tavelures ne se superposent pas.
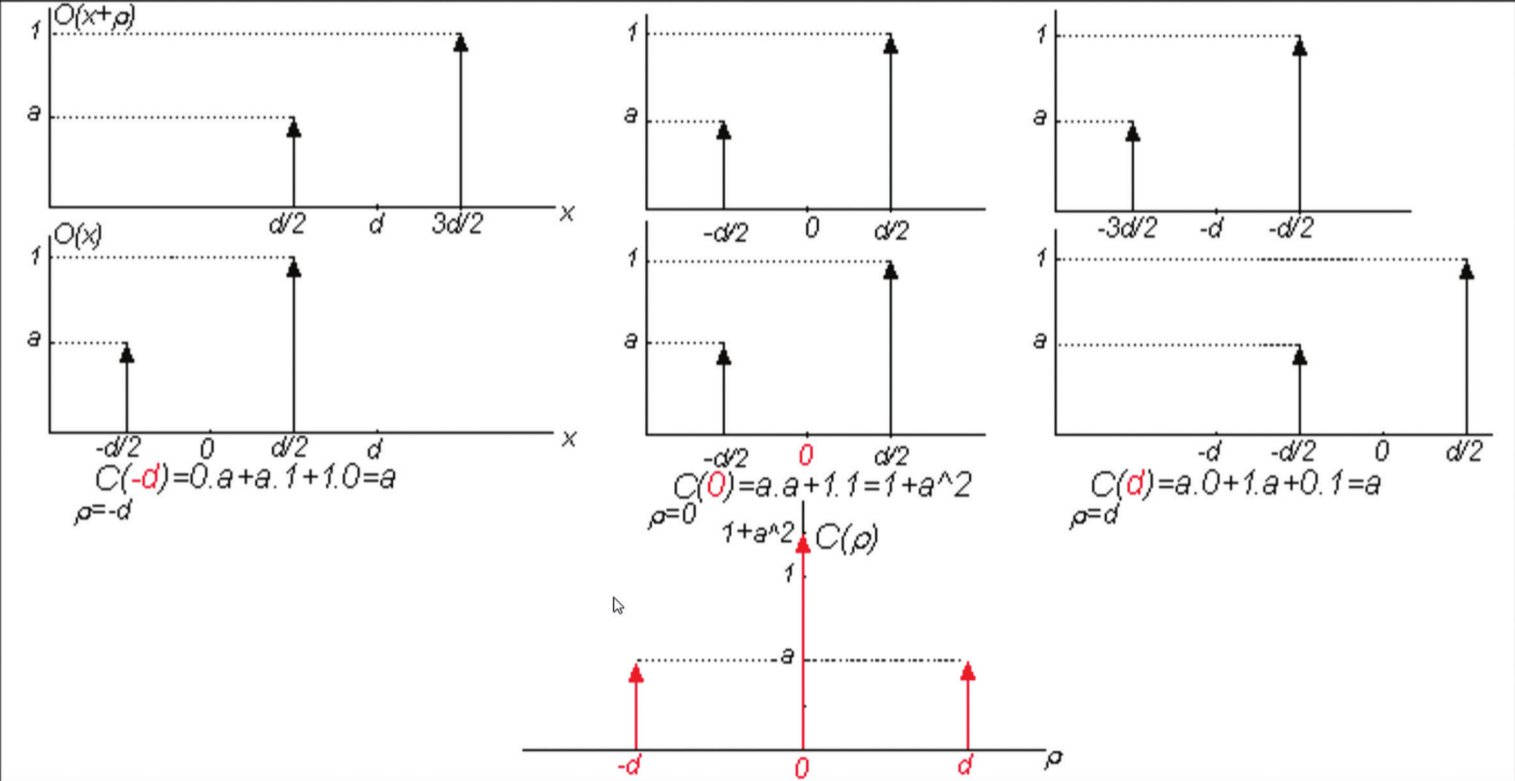
Figure 16 : Principe de l’auto-corrélation
Supposons maintenant, pour simplifier, que l’on fasse glisser les deux images dans l‘axe des deux étoiles du couple considéré. En appelant d la distance entre les deux étoiles du couple, donc entre les deux réseaux de tavelures, on considère sur la figure 16 la ligne du haut comme étant l’image que l’on décale par rapport à la deuxième ligne correspondant à l’image fixe. Le couple d’étoile est constitué de deux composantes dont celle de gauche est moins lumineuse que celle de droite. A chaque décalage, on multiplie l’image source avec l’image décalée. Comme dit précédemment, tant que les réseaux ne se superposent pas, le produit est nul. On reporte en fonction du décalage, la valeur de ce produit sur un graphe d’auto corrélation (figure 16 troisième ligne). Mais lorsque le réseau de tavelure de l’étoile 1 se superpose avec le réseau de l’étoile 2, le produit n’est plus nul, et l’on obtiens alors le pic de gauche dans le graphe de la troisième ligne. Continuons le décalage, jusqu’au moment ou le pic de l’étoile 1 sur l’image glissante se superpose à l’étoile 1 sur l’image fixe, on obtiens le pic central ou les deux images sont parfaitement superposées. Enfin, si l’on continue le décalage, le pic de l’étoile 2 de l’image glissante se superpose au pic de l’étoile 1 de l’image fixe. On obtiens alors sur le graphe du bas, 3 pics dont la séparation entre celui du centre et ceux alentours correspond à la séparation du couple qui aura donné naissance au réseau de tavelures. Cette méthode donne de très bon résultats lorsque les tavelures (qui remplacent les pics de notre exemple) sont bien marquées, à savoir lorsque . Une séquence vidéo complète ne contiens généralement pas que des réseaux de tavelures ou la condition d’isoplanétisme est respectée. Mais d’une manière générale, si l’on applique ce calcul à chaque images d’une séquence vidéo d’étoile double tavelée, et que l’on fait la somme des auto corrélations, on obtiens les 3 pics avec un rapport signal sur bruit suffisant pour établir une mesure fiable. Mis en application en deux dimensions sur un couple réel, la fonction d’auto corrélation image donne la figure suivante :

Figure 17 : Auto corrélation et inter corrélations sur couple étalon et couple mesuré
Les tavelures précédentes ont été obtenues sur Epsilon2 Lyr (étoile étalon) et Zéta Bouvier au T60 du pic du midi. On voit immédiatement les pics d’autocorrélation (colonne du milieu) qui permettent d’établir une mesure. Un raffinement supplémentaire pour améliorer le rapport signal sur bruit consiste à faire non pas la somme des auto-corrélations mais celles des inter-corrélations d’une image avec l’image au carré. Cela a pour effet d’améliorer le rapport signal sur bruit sur une séquence complète, ainsi que de lever une ambiguïté de l’auto-corrélation, à savoir laquelle des deux étoiles est la plus brillante (ou la moins brillantes) ce qui lève l’incertitude sur l’angle de position. Mais tout ceci sera traité lors du prochain article concernant la mise en œuvre pratique de l’interférométrie des tavelures.
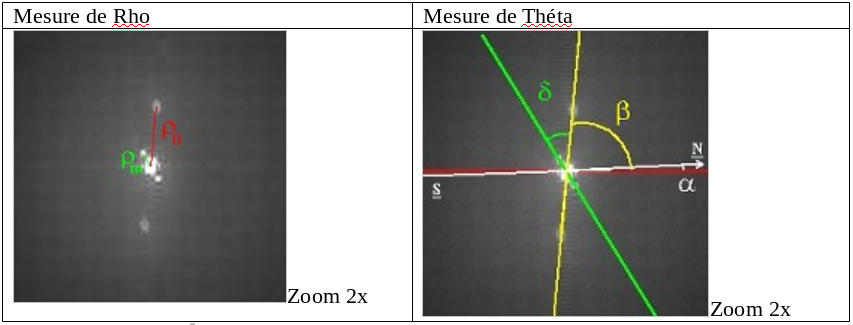
Figure 18 : mesure de séparation et angle de position avec couple étalon
Conclusion :
Dans cette première partie nous avons vu quelle est la nature physique des tavelures et comment elles se forment par un phénomène physique d’interférences constructives ou destructives au foyer d’un télescope après perturbation d’un front d’onde émis par un étoile et bosselé par la turbulence atmosphérique. Nous avons vu aussi que sous certaines conditions de turbulence atmosphérique, le réseau de tavelures est produit de manière identique par chaque étoile d’un couple d’étoiles doubles, et que l’on peut ainsi mathématiquement remonter à la position respective, de chacune des composantes du couple dans l’image. Dans l’article suivant, nous verrons quelles modalités pratiques mettre en œuvre dans le détail afin d’effectuer des mesures limitées par le pouvoir de résolution d’un instrument et non pas seulement par les conditions atmosphériques du moment.
Bibliographie :
[1] M. FRANCON, S. SLANSKI « Cohérence en optique » 1965, Éditions du CNRS [2] F. RODDIER, P. LENA « Long-baseline Michelson interferometery with large ground-based telescopes operating at optical wavelength I » 1984, Journal of optics (Paris) Vol 15, n°4. pp. 171-182 [3] C. RODDIER, F. RODDIER « Interferogram analysis using Fourier transform techniques » 1987, Applied optics, Vol 26, n°9 p1668-1673 [4] D.L. FRIED « Limiting resolution looking down through the atmosphère » 1966, Journal of the optical society of america, Vol 56 n°10 pp. 1380-1384 [5] F. RODDIER « Les effets de la turbulence atmosphérique sur la formation des images visibles et infrarouges » 1979, Journal of optics (Paris) Vol 10, n°6, pp.299-303 [6] D.L. FRIED « Optical resolution through a randomly inhomogeneous medium for very long and very short exposures » 1965, Journal of the optical society of america, Vol 56 n°10 pp. 1372-1379 [7] D.L. FRIED « Statistic of a geometric representation of wavefront distortion » 1965, Journal of the optical society of america, Vol 55 n°11 pp. 1427-1435 [8] J. VERNIN, C. MUÑOZ-TUÑON « Measuring astronomical seeing: the DA/IAC DIMM » 1995, Publication of the astronomical society of pacific 107, pp. 265-272 [9] D. BONNEAU « Expérience acquise en interférométrie optique à 2 télescopes » 1979, Journal of optics (Paris) Vol 10, n°6, pp.311-316 [10] R HANDBURRY BROWN « The Intensity Interferometer » 1974, Taylor & Francis Ltd [11] C.RODDIER, F. RODDIER « Seeing effect removal in a Michelson Interferometer » 1976, J. Opt. Soc. Am., vol. 66, n°12, December [12] F. D. EATON and Al, « Isoplanetic angle direct measurments and associated atmospheric conditions » 1985, Applied Optics, Vol. 24, n°19, October [13] J. KRAUSE-POLSTROFF and Al, « Instrument comparison : corrected stellar scintillometer versus isoplanometer » 1993, Applied Optics, Vol. 32, n°21, July [14] G.C. LOSS, C. B. HOGGE, « Turbulence of the upper atmosphere and isoplanetism »1979, Applied Optics, Vol. 18, n°15, August [15] A. TOKOVININ, « Turbulence profiles from the scintillation of stars, planets and moon » 2007, Workshop on Astronomical Site Evaluation, RevMexAA, 31, 61-70 [16] D.L.FRIED « Probability of getting a lucky short-exposure image through turbulence » 1978,Journal of the optical society of america, Vol 68 n°12 pp. 1651-1658 [17] M. SARAZIN, F. RODDIER « The ESO differential image motion monitor » 1990, Astronomy & Astrophysics. 227, 294-300 [18] C. VILADRICH « Turbulence et Seeing » 2012, Rencontres du Ciel et de L’espace Octobre 2012 [19] A. Rondi S. Rondi « Imagerie des étoiles doubles par intercorrelation », 2006, site web : http://astrosurf.com/rondi/binary_cross-correl.htm [20] E.Aristidi, M.Carbillet, J-F.Lyon and C.Aime. « Imaging binary stars by the cross-correlation technique » Astronom. Astrophys. Supp Ser. 125, 139-148 (1997)