Sommaire
Introduction :
La turbulence atmosphérique constitue le facteur majeur de dégradation des images astronomiques acquise au niveau du sol, qu’il s’agisse d’images faites avec des moyens professionnels ou amateurs. Mais comment peut on se représenter simplement les phénomènes physiques de dégradation des images par la turbulence.
La première notion incontournable dont nous avons besoin de prendre conscience est la nature propre de la lumière, et plus particulièrement sa nature ondulatoire. Par définition la lumière est une radiation électro-magnétique ,c’est a dire un rayonnement faisant intervenir un champ magnétique et un champ électrique,et dont on peut étudier les effets soit par la mécanique classique (la lumière est associée à une particule : le photon) ,soit par la mécanique ondulatoire (la lumière est associée à une onde).
Chaque particule de lumière c’est à dire chaque photon est porteur d’une quantité d’énergie notée E et dont la valeur dépend des caractéristiques de l’onde associée à ce photon. La formule donnant l’énergie du photon est la suivante :
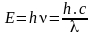
avec h est la constante de Planck, c la vitesse de la lumière dans le vide,nu est la fréquence de l’onde, et lambda la longueur d’onde
Pour expliquer ce qu’est une onde prenons l’exemple de la surface d’un liquide au repos.
Si l’on laisse tomber une goutte d’eau sur cette surface, on constate que le liquide se recouvre de cercles concentriques (on peut voir ci dessous 1/4 des cercles concentriques et le centre d’excitation de la surface du liquide). Si de plus on regarde cette surface par la tranche on observe le schéma ci-dessous :
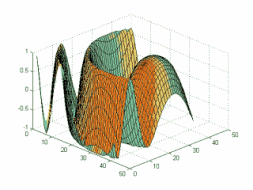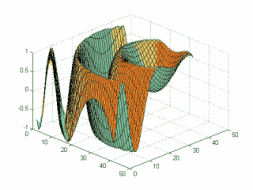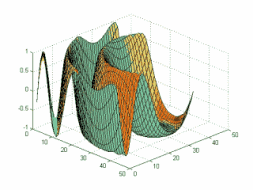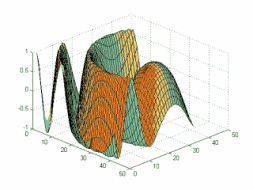
La longueur d’onde est la distance ,exprimée en mètres entre deux sommets ou deux creux de cette onde. Supposons maintenant que l’on pose un bouchon à la surface du liquide et recommençons l’expérience précédente. Lorsque la surface du liquide entre en oscillation ,on constate que le bouchon n’est soumis qu’a des mouvements verticaux :
il ne fait que monter ou descendre sans se déplacer par rapport à sa position d’origine. On appellera fréquence de l’onde le nombre de passage du bouchon par sa position la plus haute (ou la plus basse , ce qui revient au même) et par unité de temps. C’est en fait le nombre d’oscillation d’un point du liquide par seconde.
L’amplitude de l’onde,est égale à la hauteur maximum atteinte par la bouchon lors de son déplacement verticale. Lorsque l’ on se place dans le vide ,et que l’on fait varier l’amplitude d’un champ électrique et d’un champ magnétique de la même manière que l’on a fait varier la hauteur de la surface de l’eau tout à l’heure ,on produit des photons .
On peut définir le front d’onde comme étant l’ensemble des points de la surface de même hauteur, par exemple l’ensemble des « maxima » de l’onde. On peut d’ailleurs noter que la direction de propagation de l’onde défini la direction du rayon lumineux équivalent, que l’on utilise dans le cas de l’optique géométrique. Pour être parfaitement rigoureux, la définition du front d’onde qui nous intéresse est liées non pas à la vitesse de la lumière mais à une notion plus fine que l’on appelle la vitesse de groupe (http://fr.wikipedia.org/wiki/Vitesse_d%27une_onde). Sur le principe, on peut considérer que la définition précédente (ensemble des points de la surface de même hauteur) est correcte.
La phase se défini comme l’avance ou le retard de propagation de cette onde lors de sa propagation dans l’espace, depuis l’émission par la source dans un cas idéal. En effet, sans perturbation de la vitesse de propagation du front d’onde, la phase de l’onde reste constante, et la forme du front d’onde n’est alors pas déformé par le milieu dans lequel il se propage.
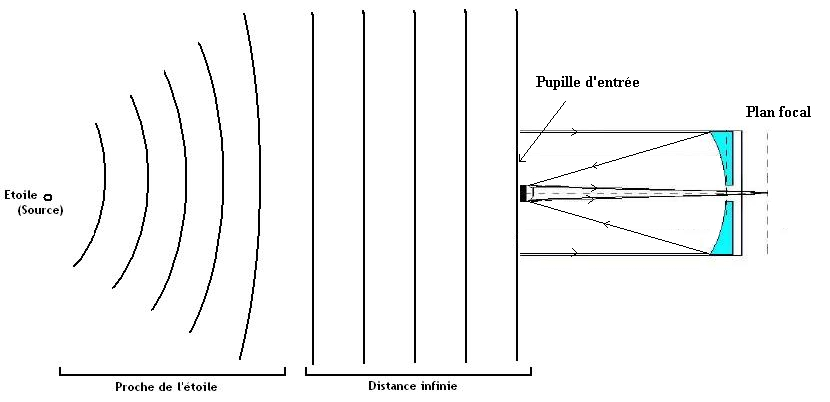
Pour comprendre cela, plaçons nous dans le cas idéal d’une source quasi ponctuelle située loin du système d’acquisition.
Une étoile peut être, en première approximation, et vu la distance à laquelle elle se situe, considérée comme une source ponctuelle. Une source ponctuelle constitue un émetteur de front d’onde circulaire. Après avoir parcouru une distance grande devant la longueur d’onde, le front d’onde incident peut être approximé comme une onde plane. Ainsi un télescope situé dans l’espace verra arriver sur son collecteur (on appelle couramment d’ailleurs l’entrée du système optique la pupille) un front d’onde plan :
En théorie, donc, l’image de l’étoile, formée par le télescope et obtenue au foyer de ce dernier sera une figure appelée tache d’Airy, et dont le profil se calcule en utilisant les lois de la diffraction (image de gauche) :
 |  |
| Image instantanée d’un point (pas de perturbation de phase) =Tache d’Airy | Image instantanée d’un point (avec perturbation de phase) =Étalement |
Causes physiques de la turbulence :
Malheureusement, les télescopes dont nous disposons sont rarement situés en dehors de l’atmosphère. La couche d’air située entre nous et l’espace est turbulente, au sens ou l’indice de réfraction de l’air http://fr.wikipedia.org/wiki/Indice_de_réfraction (c’est à dire le rapport de la vitesse de propagation dans le vide à la vitesse de propagation dans le milieu transparent) n’est pas constant sur la totalité du trajet de l’onde. On peut dire que la vitesse de formation de l’onde va ralentir en traversant le milieu transparent (cela est vrai dans n’importe quel matériau transparent). En supposant le matériau traversé complètement homogène, tout les rayons lumineux verraient leur propagation ralentie de manière homogène et le front d’onde resterai plan. Comble de notre infortune, l’indice de réfraction de l’air varie de manière aléatoire en fonction de la pression la température et la densité de l’air traversé :

Les inhomogénéïtés de pression (statique et dynamique, c’est à dire le vent), de température et de pression de vapeur d’eau vont modifier la vitesse de propagation de l’onde au cours de la traversée des couches turbulentes. La vidéo montrant les fluctuations d’indice est faite en utilisant la technique de contraste de phase. :

Une magnifique illustration du phénomène en conditon réelle, nous est donnée par le cliché suivant (réalisé par Trevor Mahlmann) montrant une fusée Falcon 9 de SpaceX au décollage et en contre jour façe au Soleil. Comme nous pouvons le voir sur les couches d’air au dessus d’une route surchauffée en été, ici les gaz chauds éjectés par les moteurs de la fusée surchauffent localement l’air, provoquant ainsi la génération de bulles de turbulences optique dues aux différences d’indice de réfraction entre l’air chaud et l’air plus froid :

Les bases mathématiques de la décomposition spatiale de la turbulence ont été étudiées par le mathématicien russe Kolmogoroff (Kol 1941) qui a défini l’échelle minimale d’une cellule de turbulence comme suit : Dans un fluide en mouvement ,l’échelle minimale d’une cellule de turbulence est donnée par la dimension de Kolmogoroff. Cette dimension ne dépend que de la viscosité du fluide (n) et de son énergie cinétique par unité de masse (e)
 |  |
Il en découle directement qu’a l’échelle de la cellule de Kolmogoroff, la viscosité domine et l’énergie cinétique du fluide est dissipée en chaleur. Les deux conséquences directes en sont que :
– Plus la température locale augmente, plus les cellules sont petites,
– Plus la cellule est chaude, plus elle évolue vite
Comprenant alors la dynamique du fluide atmosphérique, Tatarski (1961) effectue la transposition de la modélisation des cellules de turbulence au sens de Kolmogoroff en terme de variations des indices optiques (vues précédement), pour modéliser les effets de déformation du front d’onde dût à la variation de phase avant d’arriver sur la pupille du télescope.
Lors de la traversée de zones plus ou moins dense (ou chaude ou froides), les points du front d’onde sont plus ou moins ralentis, ce qui affecte la forme générale du front d’onde au moment de l’arrivée sur la pupille du télescope. Toute l’analyse que l’on peut faire des effets de la turbulence résulte des caractéristiques de déformation de ce front d’onde par rapport à la pupille…
La déformation du front d’onde à l’arrivée sur la pupille est donc la résultante de déformation par les fluctuations d’indice intégrées du sol à l’espace (Fonction de structure du front dépendant du profil de la turbulence en altitude (C²n(z) avec z l’altitude de la couche turbulente).
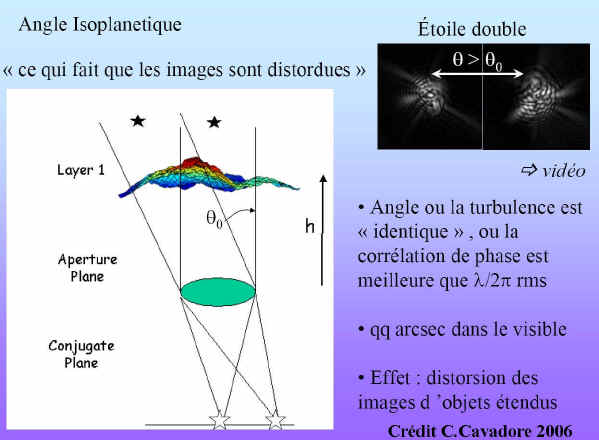
Différents effets de la turbulence :
Les conséquences directes de déformation du front à l’arrivée sur la pupille sont des effets de courbure à différentes échelles spatiales du front d’onde. La turbulence se décompose alors de manière assez simple en considérant la taille de l’objectif du système d’acquisition (pupille) par rapport à la dimension angulaire de la perturbation atmosphérique.
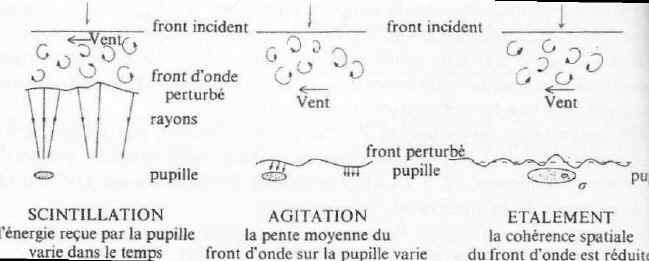
En partant des objectifs de diamètre le plus petit, jusqu’au diamètre les plus grands, on peut décomposer la turbulence suivant les 3 phénomènes prépondérants simples suivant :
– La Scintillation (D<100mm): Il s’agit de la fluctuation de l’éclat d’une étoile, lorsqu’elle est observée avec l’œil ou une pupille de petit diamètre (nous verrons plus loin l’ordre de grandeur de diamètre de cette pupille). La scintillation correspond à un étalement ou une concentration de l’énergie du front d’onde. En d’autre termes, la turbulence dans l’axe de visée, provoque un effet de lentille qui peut être soit convergente, soit divergente, et ce avec une variation dans le temps généralement rapide (voir plus loin).
On peut d’ors et déjà remarquer que la scintillation n’est observée que sur les étoiles (sources quasi-ponctuelles) et non sur les planètes, qui sont des sources plus étendues (quelques secondes d’arc à quelques dizaines de secondes d’arc). Il existe donc un angle sous tendu par la source pour lequel la perturbation du front d’onde ne peut plus être considérée comme uniforme (si tel était le cas, la scintillation resterai uniforme). On parle alors de perte de cohérence des rayons issus de la source. Cet angle s’appelle l’angle d’isoplanétisme(Théta0). Nous en verrons une définition plus précise un peu plus loin.
– L’agitation (100mm<D<250mm): Il s’agit de la variation au cours du temps de l’angle du plan moyen tangent au front d’onde par rapport au plan de la pupille. Cet angle d’incidence du front d’onde sur la pupille, provoque un déplacement de l’image. Ces fluctuations de positions du centre de l’image sont aussi connues sous le nom de « Tip-Tilt« . Appelons la grandeur caractéristique de ce phénomène le temps de cohérence tau‘0
Lors de l’intégration d’une pose longue en imagerie astronomique, ces fluctuations de positions sont, pour les diamètres d’instruments amateurs (entre 10 et 25cm), responsables de la majorité de la dégradation de la taille d’une source ponctuelles (nous en feront une démonstration plus loin). C’est entre autres ce qui définit une largeur d’étoile a mi hauteur, sur l’image acquise, supérieure au diamètre théorique de la tache d’Airy obtenue avec un télescope de moyenne gamme
– L’Étalement (D>250mm): C’est le phénomène qui conduit, pour les ouvertures dont le diamètre est important, à des images d’étoiles de dimension largement supérieure à celle qu’imposerai le critère de diffraction. C’est la chose que nous avons vu au début de cette page (l’ordre de grandeur est de la seconde d’arc). Ceci est dût a ce que l’on appelle la perte de cohérence spatiale sur la pupille d’entrée du télescope, cela veut dire que la désorganisation du front d’onde est telle que deux front d’ondes qui devrait être séparés par une longueur d’onde, finissent par se rejoindre le long d’un contour fermé dans la surface de la pupille. La zone délimitée par ce contour est appelée zone de cohérence, et sa dimension est donnée par un paramètre nommé r0, le diamètre de la tache de Fried.
Nous avons donc énoncé ici les principales définitions relatives aux déformations liées à la turbulence atmosphérique et aux dégradations de l’image.
Pour bien comprendre chacun de ces phénomènes physiques, il va être nécessaire de les décomposer l’un après l’autre et regarder pour chacun dans quel cas le diamètre d’un objectif donné sera influencé par l’un ou l’autre de ces phénomènes.
La Scintillation – L’angle d’Isoplanétisme :
La scintillation est le premier facteur de turbulence auquel l’atmosphère terrestre soumet l’observateur. L’observation des étoiles à l’oeil nu nous montre que l’éclat apparent des étoiles varie plus ou moins rapidement dans le temps. Ce phénomène que les anglo-saxons appèlent « twinlkling » apparaît donc avec un instrument d’acquisition de petit diamètre : la pupille de l’oeil, soit environ 6mm de diamètre lorsque l’accoutumance à l’obscurité est réalisée.
La cause physique décrivant la scintillation est la variation du rayon de courbure moyen du front d’onde à l’arrivée sur la pupille, comme pourrait le produire une lentille divergente ou convergente (si la pupille est de petite dimension (inférieure a 10cm)) Tokovinin 2006.
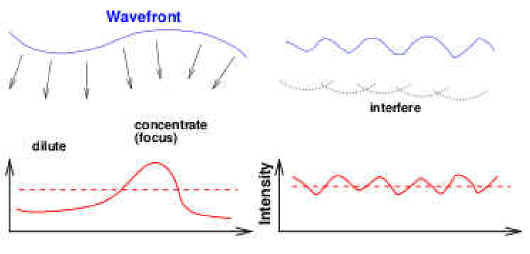
Pour citer A. Tokovinin [1] : « La Scintillation des étoiles est la plus évidente des manifestations de la turbulence optique qui causent l’appréciation du « Seeing ». Pourrait-on alors utiliser une mesure quantitative de la scintillation pour estimer la valeur du « seeing »?… «
L’un des premier essais d’extraction du profil vertical de la turbulence en mesurant la scintillation a été réalisé en 1976 par Ochs et Al. Il a été établi plus tard qu’en fait, la scintillation est trés étroitement corrélée à l’angle d’isoplanétisme (Krause&Polstorf 1993).
Pour illustrer ce qu’est l’angle d’isoplanétisme, prenons l’exemple concret d’une étoile double de séparation epsilonr :
Exemple Gamma Virgo : Séparation epsilonr = 1 »4
– si la séparation du couple est inférieure à l’angle d’isoplanétisme, les 2 figures de diffraction (fonction d’étalement) seront identiques
– si la séparation du couple est supérieure à l’angle d’isoplanétisme, les 2 figures de diffraction seront différentes
 |  |
| epsilonr<Théta0 | epsilonr>Théta0 |
Théta0 est la zone au sein de laquelle la fonction d’étalement est « identique ». Autrement dit si les deux composantes du couple sont comprises dans cette zone, chaque composante va produire une fonction d’étalement similaire. C’est le cas pour l’image de gauche (on a 2 psf quasi identique avec une tavelure en forme de virgule au dessus). On est dans le cas ou epsilonr<théta0. Par contre, dans l’image de droite, la zone d’isoplanétisme est plus petite que la séparation du couple (epsilonr>théta0). Chaque composante va produire son propre schéma de tavelures, ici plus étalé, et ne ressemblant pas a celui de sa voisine. La superposition des 2 fonctions d’étalement donne l’impression qu’elles sont confondues, mais il s’agit bien de la superposition de 2 fonctions d’étalement différentes.
Les professionnels, dans le cadre de campagnes de mesures destinées à déterminer le meilleur site d’implantation d’un télescope, se sont plus particulièrement penchés sur les profils de turbulence atmosphériques, en fonction de la hauteur de la couche turbulente. Ce fut pour eux l’occasion de développer un certains nombre de méthodes de mesures dont certaines étaient basées sur la mesure de la scintillation d’une étoile.
Il a été démontré par Vernin et Al, que les altitudes respectives des couches turbulentes traversées, peut être analysées sur la base de la scintillation d’étoiles doubles judicieusement choisies (Scidar).
On peut trouver dans la littérature quelques instruments de mesure d’angle d’isoplanétisme chez les professionnels :
– Scidar (Vernin & Al)
– Generalised Scidar (Fuchs & A 1998)
– Single star Scidar (Habib & Al 2006)
– MASS (Kornilov & Al 2003)
Tous ces appareils (qui ne sont autre que des photomètre rapides) ont pour point commun de mesurer une quantité appelée index de scintillation.
 |  |
| Mode direct | Mode différentiel |
Avec IA l’intensité à l’instant t et Delta(IA) la variation de cette intensité entre deux instants.
Comment s’établit alors la relation entre l’angle d’isoplanétisme et l’index de scintillation. d’après Tokovinin ([Tok98]), l’expression de l’index de scintillation est donnée par la relation (la notation sA et sigmaI sont équivalentes) :
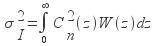
Avec C²n(z) le profil d’index de réfraction en fonction de l’altitude, et W(z) une fonction de pondération dépendante aussi de l’altitude :
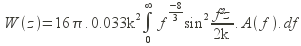
avec
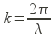
le nombre d’onde, et
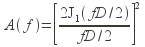
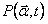 la fonction pupille
la fonction pupille
Or d’après Eaton & Al, l’angle d’isoplanétisme s’exprime sous la forme :
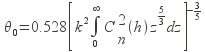
De la même manière, d’après Krause et Polstroff :

avec Phi l’angle zénithal
En supposant que la fonction de pondération W(z) peut être approximée par une fonction en z^3/5,
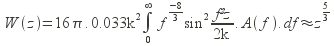
Alors, et seulement a cette condition, on peut établir la relation [1] :
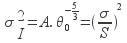
Il existe donc une relation directe liant la variance de l’indice de scintillation, et l’angle d’isoplanétisme, à une constante près, mais dont la valeur dépend de l’altitude de la couche turbulente.
En première approximation, (Eaton & Al 1985), on considéré cette constante indépendamment de l’altitude (A proche de 1µrad). Mais une analyse plus fine (Vernin & Al) à montré que la valeur exacte de A dépendait de W(z). Pour s’affranchir de cette dépendance, une solution est de mesurer l’indice de scintillation en mode différentiel en choisissant judicieusement des diamètres de pupille annulaire. L’indice différentiel de scintillation permet de se rapprocher de la condition de quasi indépendance de A à W(z).
C’est ce qui a permis de mettre au point chez les professionnels, entre autre le MASS :
 |  |
L’étude des indices différentiels respectifs des pupilles A, B, C et D permet de remonter a la valeur exacte de Théta0
En tout état de cause, le segmentateur reste un dispositif délicat à fabriquer, et une mesure trés précise devrait alors se baser sur un instrument multiple dont les ouvertures de pupilles respecteraient les conditions du MASS et de l’invariance a W(z).
Du point de vue amateur, on peut ne pas perdre de vue que l’intérêt de la mesure de l’angle d’isoplanétisme réside dans la sélection des images pour lesquelles cet angle d’isoplanétisme est le plus grand possible. Autrement dit en se contentant d’une mesure mono-pupille, est-il possible d’en tirer une information sur l’image d’une séquence video et plus particulièrement de sélectionner les images à grand Théta0?
C’est sur la base de cette hypothèse, et en utilisant l’approche de Eaton & Al que nous avons mené quelques expériences de mesure de la scintillation :
Quels moyens amateurs peut-on mettre en oeuvre pour y parvenir :
– Cameras rapides et sensibles (poses très courtes <20ms)
– Optiques de petit diamètres (<10cm) type objectif d’appareil photo)
– Un peu d’huile de coude pour le traitement et un bon soft de traitement (Iris, Prism) si on procède en post-traitement
– Un tableur pour le traitement statistique des données.
Tout cela manque un peu d’automatisation, mais cela ne saurait tarder.
Pour ce qui est de cameras sensible et rapides, le premier essai sur l’étoile Alnilam à été réalisé avec une Basler 640, un objectif f= 35mm, D= 56mm
 |
Une solution passant par une camera EMCCD, High cost, mais extrêmement efficace permet de proposer une analyse multicible sur un champs large :
 |  |
10 images par secondes (Video de 30 secondes)
Pour tenter de mesurer la scintillation et par la même l’angle d’isoplanétisme, nous avons procédé comme suis :
Dans un premier
– Pour chaque image (numérotée n), on extrait l’intensité à l’instant t en utilisant la relation des magnitudes pour remonter au flux lumineux.
– Calcul de l’indice de scintillation monopupille avec les valeurs à t-t0 et t+t0, ou t0 est l’intervalle entre 2 poses
Un essai a été fait aussi avec la statistique de la distribution d’intensité en considérant 5 échantillons autour de l’instant t de l’image n. Les résultats sont cohérents avec la première méthode.
– Calcul de Théta0 à l’instant t
Par la Relation => On obtient immédiatement l’estimation de Théta0 et l’identification images ou Théta0est maximal. Les graphes ci-dessous sont en échelle logarithmique, Théta0exprimé en secondes d’arc.
 |
 |
La courbe d’isoplanétisme montre que la valeur instantanée de Théta0 peut prendre des valeurs trés grandes sur des temps extrêmement courts (pour mémoire, la video prise à 25 images par secondes, poses de 10ms situe 5 échantillons dans un intervalle de 200ms. Cela sous tend que le temps de stabilité de Théta0 peut être grand devant la pose si cette dernière est trés courte (20ms ou moins).
L’avantage de l’utilisation d’une camera EMCCD est de pouvoir poser suffisament court et d’avoir une détectivité suffisante pour imager simultanément des étoiles séparées par des distance angulaires importante. On pourrait d’ailleurs imaginer monter une manip de détection multicible avec 3 cameras EMCCD travaillant avec des objectifs de différents diamètres (pour faire de la scintillométrie différentielle sur chaque étoile) pour obtenir une cartographie de l’évolution de l’angle d’isoplanétisme dans le temps, sur un champ large.
Malheureusement, il apparaît que le prix d’une EMCCD empêche l’amateur de tenter l’expérience. A défaut, et disposant d’une EMCCD en prêt par la société Raptor Photonics, nous avons tenté une mesure simultanée sur l’ensemble des étoiles du champs pour lesquelles le rapport signal sur bruit était suffisant. Le mesure d’angle d’isoplanétisme des 5 premières cibles du champ est montrée sur la figure de gauche. On s’aperçoit d’emblée qu’il n’y a aucune cohérence temporelle dans les 5 directions mesurées. Cela semble logique connaissant l’ordre de grandeur de l’angle d’isoplanétisme (quelques secondes à quelques minutes), au regard des quelques minutes a quelques degrès séparant les étoiles du champ. Toutefois, histoire d’observer physiquement la vitesse d’évolution de l’angle d’isoplanétisme, nous avons procédé à une interpolation spatiale des valeurs des angles mesurés pour 15 étoiles du champs identifiés sur l’image de droite, ainsi qu’a une interpolation temporelle de manière a fluidifier le ralenti.
 |  |
Sans prétentions particulière, cette interpolation est la démonstration pédagogique du fait qu’il est délicat voire quasi impossible de vouloir compenser de manière simultanée l’effet de la turbulence sur un grand champs, chaque zone d’isoplanétisme ayant une turbulence décorrélée de sa voisine (donc des propriétés propres en tau’0 et r0 différentes).
Que nous montre l’analyse statistique de la turbulence sur cette séquence video. Si l’on regarde les histogrammes obtenu des 5 cibles analysées, on peut voir les graphes suivants :
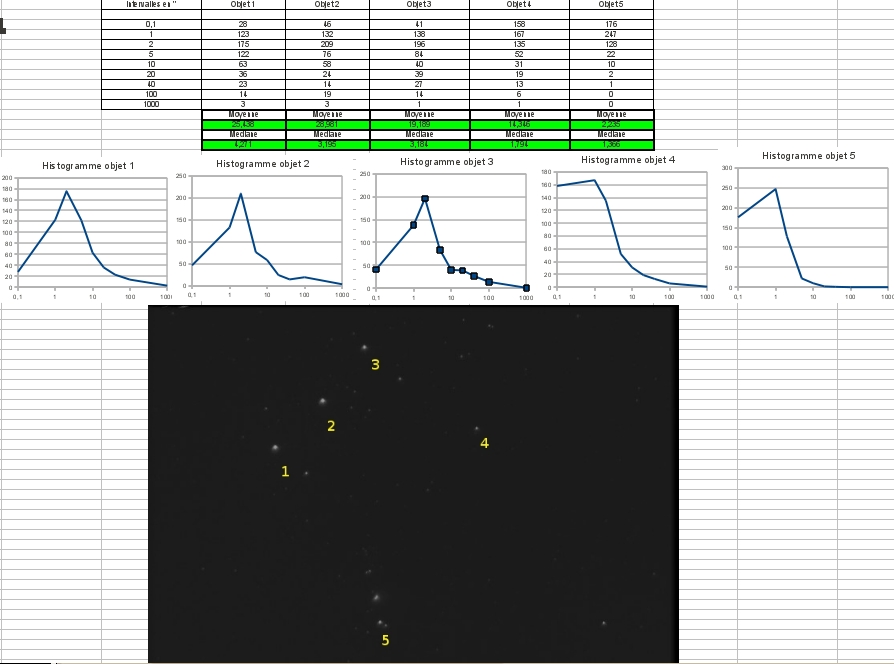
Les valeurs médianes obtenues son comprises entre 1″36 et 4″ 27. Nous sommes donc dans les ordres de grandeur des mesures de valeurs médianes de q0 effectuées par les professionnels, comme celle présentée en suivant, réalisé par Ziad & Al en 2004 au mont Palomar (1″96) :
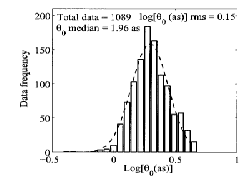
Quantitativement, les mesures que nous avons effectuées sont dans l’ordre de grandeur, et ce qui est surtout remarquable, c’est de voir des angles dépassant plusieurs dizaines de secondes d’arc, sur des temps voisin de 40ms. Nous sommes donc avec des caméras rapides, en sélectionnant les bonnes images, dans des conditions optimales d’isoplanétisme.
On peut donc dire en conclusion sur la mesure de l’isoplanétisme que C’est une bonne méthode de vérification de qualité de site, et de sélection d’image sur source ponctuelles (étoiles doubles) mais peut on s’en servir en planétaire ?
– A priori oui, mais difficile à mettre en oeuvre directement sur l’objet car la source n’étant pas ponctuelle, la scintillation planétaire est diluée (1e-4 pour les planètes, 1e-8 pour le Soleil)
– Il faut descendre le diamètre de pupille collectrice (de l’ordre du rayon de Fresnel quelques cm) donc avoir des caméras très sensibles !!
– La réponse de l’instrument devient fortement dépendante de l’altitude de la couche turbulente (principalement sensible au premier km d’atmosphère), la mesure exacte sera entachée de l’incertitude sur le comportement du W(z) vu précédemment.
On peut noter en dernier lieu que des méthodes professionnelles de mesure de scintillation planétaire, lunaire ou solaire existent (PlaSci, LuSci (Tokovinin 2005), Shabar (Beckers 2001)) Mais ces dernières ne permettent pas intrinsèquement de s’en servir comme moniteur de Seeing généralisé.
Dans la zone d’Isoplanétisme : Agitation (Tip/Tilt)
Si nous nous plaçons dans l’angle d’isoplanétisme, le premier effet mesurable de la déformations du front d’onde est l’effet d’agitation (Tip/Tilt), c’est à dire l’effet de déplacement aléatoire de l’image pendant la pose. Ce déplacement de l’ensemble de l’image est dût à la variation de l’angle d’incidence moyen du front d’onde a l’arrivée sur la pupille. Ce phénomène se modélise très bien en utilisant les 2 premiers ordre des polynomes de Zernikes (caractérisant les déplacements en X et en Y)
 |  |
Chaque image étant réalisée sur un temps de pose généralement supérieur à la vitesse d’agitation, on « intègre » donc le déplacement de l’image d’une étoile, la résultante étant alors une tache « floutée » par le déplacement rapide de la tache d’Airy originale.
Pour bien s’en rendre compte, on a réalisé l’expérience suivante : en utilisant un LX200 mm, diaphragmé à 90mm, et un ETX en parallèle pour l’autoguidage, une Vesta Pro enregistre une séquence video de 30 secondes (cadence d’acquisition 10 images/s). La tache d’Airy obtenue pour ce diamètre reste raisonnablement peu entachée de turbulence par étalement (voir plus loin), on peut donc obtenir une idée de l’agitation due a la turbulence si l’on s’affranchi des défauts de suivi, dont on peut avoir une idée par les décalages lents obtenus vie l’autoguidage. Les relevés de positions réelle sont donc obtenus sur la courbe suivante « Rouge ». Les défauts de suivi sont matérialisés par la courbe « Verte ».
 |  |
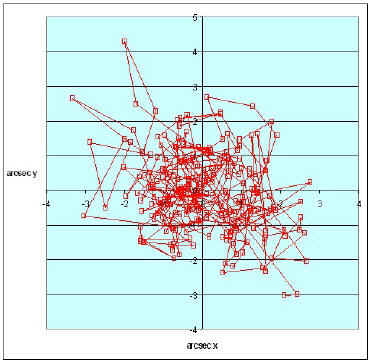
Après soustraction des défauts d’autoguidage, nous retrouvons les fluctuations rapides en X et en Y dues à la turbulence, et plus particulièrement à l’agitation (les échelles sur le graphes sont en seconde d’arc). Si nous regardons précisément durant une pose de 30 secondes, la dispersion de la position du centroïde de l’étoiles, nous obtenons en X et en Y les graphes suivants :
 |  |
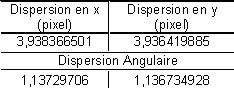
On voit immédiatement que le déplacement de l’image pendant une pose de 30 secondes provoque (pour ce diamètre de pupille), une dégradation du rayon de la tâche de diffraction (a un sigma) d’une étoile de près de 40% (1″14 contre une tache théorique de 0″8)
Quelles sont les solutions de compensation existantes ?
– Compensation soft à posteriori (registration) :
C’est la solution la plus efficace, la preuve en est avec l’utilisation de logiciels de type Iris, Prism, Registax, Autostacker, etc… – Compensation Hardware (AO7) La solution Hardware offerte par l’AO7 offre 2 inconvénients : -Sa vitesse de compensation n’est que d’une dizaine de Hertz, ce qui ne la rend pas suffisamment réactive pour compenser une turbulence dont la vitesse de variation est de l’ordre de quelques millisecondes. La vitesse de correction devrait être de l’ordre du kHz.
– La compensation est uniquement valable dans l’angle d’isoplanétisme, donc au mieux quelques dizaines d’arc secondes. Sont efficacité doit être théoriquement limitée par la taille du champs imagé.
Nous verrons plus loin que pour des pupilles de diamètre inférieur à 250-300mm, une compensation rapide du tip/tilt constitue le meilleur moyen de compenser la majeure partie de la dégradation du front d’onde.
Pour aborder la suite des perturbations du front d’onde par la turbulence, et comprendre les variables caractéristiques caractérisant cette dernière, nous avons besoin de voir ce qui se passe pour les ordres supérieurs de déformation du front.
Dans la zone d’Isoplanétisme : La fonction d’étalement :
La troisième quantité caractéristique de la déformation du front d’onde consiste en la dimension des « bosses » et de « creux » que l’on peut constater sur la structure du front d’onde, qui, rappelons le, était à l’origine plan. Ces déformations sont caractérisées, pour les spécialistes par les polynômes de Zernikes d’ordre supérieurs à 2.
En 1965, D.L. Fried introduit une quantité fondamentale : r0 (le paramètre de Fried), qui de part ses propriétés, rend compte de l’étalement de flux sur l’image obtenue d’une source ponctuelle. C’est l’indice caractéristique de la fonction d’étalement
On défini r0 le rayon de Fried comme le diamètre de la zone de la pupille pour laquelle la variation de la phase est inférieure à
 |   |
Chaque sous pupille de dimension r0 va interférer avec ses voisines, et provoquer une image instantanée étalée, et constitués d’une multitude de sous figures de diffractions dont les dimensions sont celle de la tache d’Airy du télescope en pleine ouverture. Ces grappes de lumières portent le nom de tavelures (Speckles en Anglais), et ont été mis en évidence par A. Labeyrie en 1974.
Un certain nombre de choses sont à retenir de l’effet des tavelures sur l’image d’une étoile :
– La taille de r0 est considérée comme constante dans l’angle d’isoplanétisme
– Le rapport du diamètre sur r0 caractérise la dégradation de la résolution donc l’étalement
– On peut noter que le nombre de tavelures dans une image est (D/r0)²
A la valeur r0 on fait correspondre un diamètre de zone dans la pupille, et non un rayon de zone, contrairement a ce que le nom du paramètre r0 laisse croire.
Vitesse de variation du Tip/tilt :
Le résumé complet de la situation de dégradation de l’image théorique (image simulée à gauche) par altération du front d’onde est présenté sur les images expérimentales obtenues au télescope de 60cm du pic du midi à l’aide de cameras rapides :
 |  |  |  |
| Hors atmosphère (a) | Instantanée étalement (Tavelures) (b) | Cumulée Tip/Tilt compensé (c) | Cumulée Tip/Tilt non compensé (d) |
Seule l’image de gauche est une image simulée (image (a)). A très court temps de pose (10ms : image (b)), on obtient une fonction d’étalement quasi-instantanée. Si l’on dispose d’un moyen de compensation du tip/tilt (ici la compensation a été réalisée via un software, image (c)) la pose cumulée est représentative de défauts optiques du télescope (défauts statiques dans le temps), et de la dispersion du flux lumineux dût à l’intégration des fonctions d’étalements instantanées aléatoires. On obtient alors une image d’étoile (dite aussi réponse impulsionnelle du télescope), représentative de ce que Fried appelait le « seeing longue pose« , et dont la valeur est directement liée à la distribution statistique du r0 pendant la pose. En dernier lieu (image (d)) la composante d’agitation entre en jeu et dilue encore le « seeing longue pose » via 2 causes : les défauts de suivi de la monture (dont la caractéristique principale est d’être constituées de variation lentes et facilement mesurables), et d’autre part les fluctuations rapides et aléatoire de l’incidence du front d’onde, dont la vitesse d’évolution est de l’ordre de tau’0. C’est parfois a tord que l’on qualifie de seeing longue pose la mesure de la largeur a mi hauteur constituant le résultat final d’une image CCD. Ce « seeing » mesuré est en fait la combinaison de l’intégration des fonctions d’étalements, caractérisées par les statistiques sur r0, de la composante de tip/tilt, caractérisée par tau’0, et des défauts de suivi du télescope. Trois des grandeurs caractéristiques de la turbulences sont donc r0, tau’0 et theta0 On peut alors se demander si il existe une dépendance ou une sensibilité plus importante à certains des effets d’un télescope de caractéristiques données. En 2005, Cyril Cavadore avait étudié cette dépendance en regardant de près le strehl ratio (à savoir le rapport de l’intensité du pic central hors turbulence et cette même intensité avec turbulence) en fonction de 2 paramètres : le diamètre et la valeur du r0. Le résultat était le suivant :
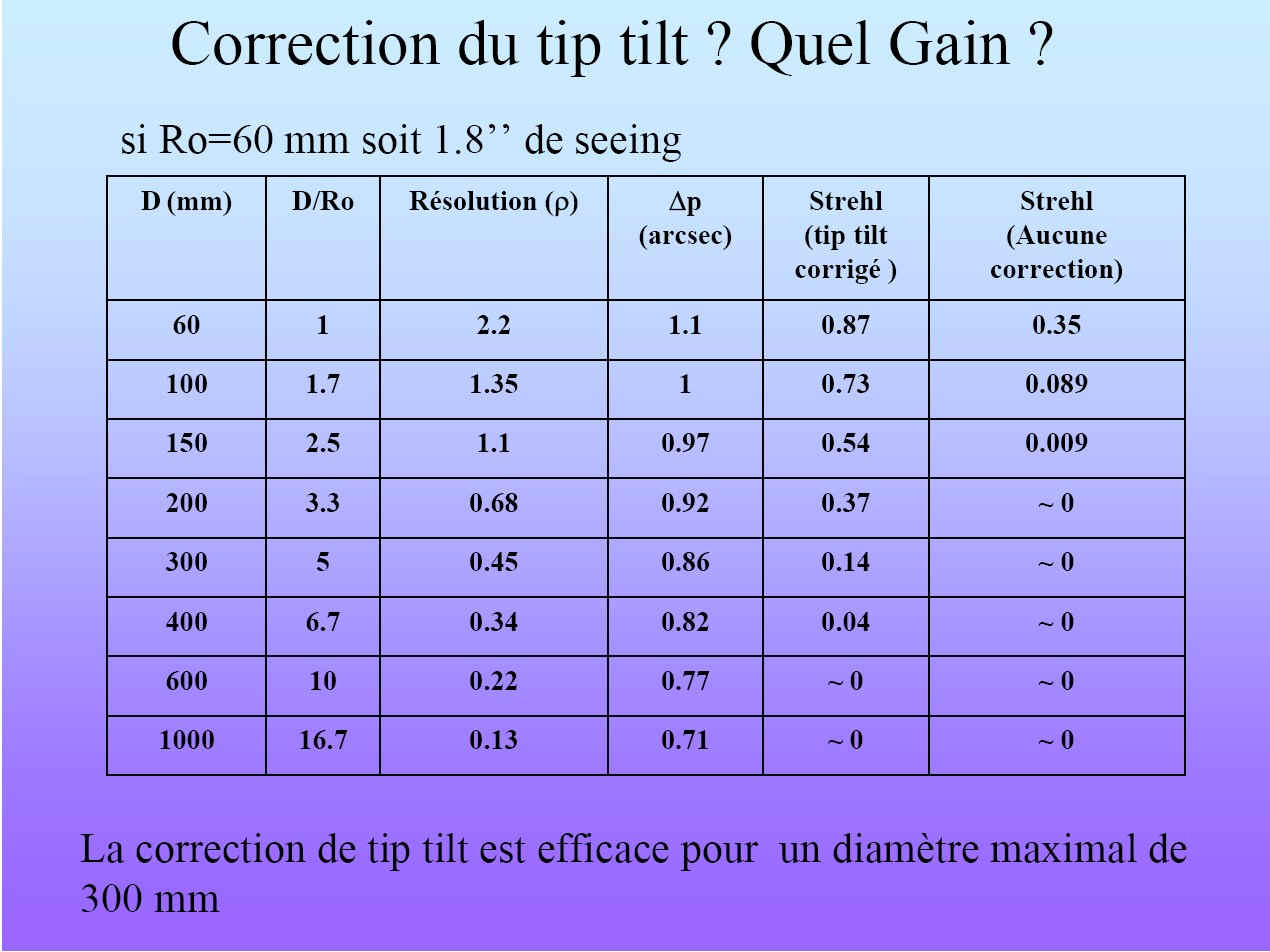
Pour un r0 de 60mm, valeur courante sur les lieux d’observations utilisés par les amateurs, le strehl ratio d’un instrument de 60mm est de 35%. Le fait de simplement corriger le tip/tilt permet d’obtenir le même strehl ratio sur des instruments de D=200. Si l’on va jusqu’a 300mm, le strehl obtenu avec compensation de l’agitation est de l’ordre de 50%. On peut donc raisonnablement considérer que la compensation du tip/tilt compense la moitié (ou plus) des effets de la turbulence pour des télescopes jusqu’a 300mm de diamètre. Au delà, c’est la fonction d’étalement qui devient prépondérante dans la dégradation des images.
C’est une conclusion essentielle, car elle montre qu’imaginer une optique adaptative à plusieurs ordre pour des télescopes de petit diamètres, est inutile, la compensation du tip/tilt fait la quasi totalité du travail.
De fait, comment caractériser la vitesse de fluctuation du Tip/Tilt.
Si nous prenons l’exemple suivant (Gamma Virgo séparation 1″4), obtenue à la lunette de 50cm de l’observatoire de Nice (camera Basler Ace 640 100ips), nous obtenons une visualisation directe de la vitesse de fluctuation de position de l’image, qui est pour des télescopes amateurs, le principe limitant principal de la turbulence.
Les tavelures sont aussi présentes, et l’on peut voir expérimentalement que la vitesse de fluctuation des tavelures, et la vitesse de variation de position de l’image, semblent corrélées.
 |  |
Le temps caractéristique de fluctuation de Tip/TIlt et le temps de cohérence des cellules de turbulence définissant la persistance des speckles ne sont pas rigoureusement la même quantité. Toutefois, en attendant de trouver la démonstration permettant de relier tau’0 et tau0, nous considéreront ces deux quantités comme équivalentes.
Si nous prenons l’exemple des publications professionnelles sur le sujet, nous pouvons voir que ces derniers ont pour habitude de publier les résultats de leurs mesures sous forme d’analyses statistiques ou la valeur le plus représentatives d’un échantillons de quelques centaines d’images est la médiane de cet échantillon. La raison en est que des valeurs trop aberrantes entachent le calcul de la moyenne d’un biais statistique par rapport à la distribution des valeurs de cet échantillon.
Les valeurs de t0 sont de l’ordre de quelques millisecondes à quelques dizaines de millisecondes.
En tant qu’amateurs, de quoi disposons nous pour mesurer quantitativement la turbulence, enfin en priorité les grandeurs caractéristiques que sont angle d’isoplanétisme, temps de tip/tilt, et rayon de Fried.
Pour le r0, Sarrazin et Roddier en 1990 et Vernin-Monuz en 1995 ont défini, chez les professionnels, un appareil appelé DIMM (Differential Image Motion Monitor), permettant de mesurer précisément le r0. DIMM signifie en français moniteur de mouvement différentiel de l’image. Son principe est basé sur la différence de mouvement de l’image dédoublée d’une étoile, le long de l’axe des x et le long de l’axe des y sur l’image.
Le principe en est simple : Un masque à 2 trous, et dont l’un des trous dispose d’un prisme à angle très faible, permet de former 2 images de la même étoile.
Sarrazin et Roddier ont montré en 1990 que la variance du mouvement différentiel des 2 images est liée a la valeur du r0 par les relations (en notant l le mouvement longitudinal et t le mouvement transversal) :
avec ![]() et
et ![]() les coefficients d’ajustement longitudinaux
les coefficients d’ajustement longitudinaux
 étant la dispersion sur chacun des axes
étant la dispersion sur chacun des axes
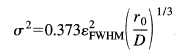
(epsilon(FWHM) étant la largeur angulaire de la PSF d’un trou seul)
Donc connaissant la variance sur chaque axes, on obtient un r0(l) longitudinal et une r0(t) dont on fait la moyenne pour obtenir r0 final. Cyril Cavadore, chez les amateurs, a développé en 2005 un logiciel permettant de faire simultanément l’acquisition et l’analyse du r0. Ce logiciel est disponible à l’adresse : http://www.alcor-system.com/us/DimmSoftware/index.html
Du coté de l’Université de Cambridge, en 2004, Senata et O’Donovan ont développé le DIMMWIT (DIMM which is transporable) dont la particularité était de permettre en mode temporel, d’accéder à la valeur de t0: http://www.mrao.cam.ac.uk/~jsy1001/dimmwit/
 |  |   |
| DIMM standart sans prisme (mode spatial) | HX516 en mode fenétré | Lecture rapide de la persistance des speckles (mode temporel) |
Ce DIMM amateur, dont le logiciel fonctionne sous linux, permet 2 modes de fonctionnement, mais non simultanés.
Peut-on alors envisager un seeing mètre amateur simple permettant d’accéder simultanément aux trois paramètres cités précédemment (théta0, r0tau0 ?).
Mesure par les franges d’Young :
L’expérience des franges d’Young, bien connue surtout pour n’avoir d’explication qu’au travers de la nature ondulatoire de la lumière, peut peut être nous ouvrir une voie pour définir un seeing mètre amateur simple. Un petit rappel sur la nature de cette expérience est nécessaire. En supposant un masque percé de 2 ouvertures laissant passer un front d’onde, et en supposant réunies les 3 conditions suivantes :
- Source monochromatique
- Onde incidente plane (source non résolue)
- Distance au plan du détecteur grande devant l’écartement des trous
Un capteur permettant de mesurer les intensités au foyer permettra d’obtenir une succession de franges claires et sombres apparaissant en fonction de la différence de marche des rayons issus du trou T1 et du trou T2.
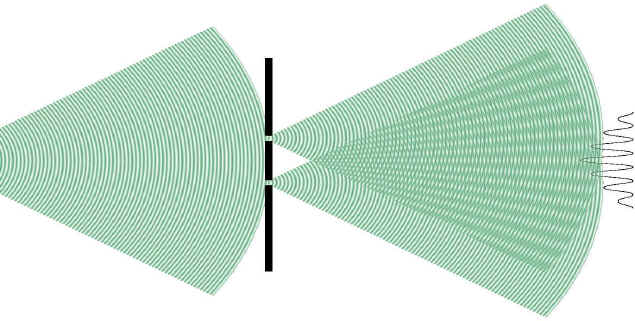
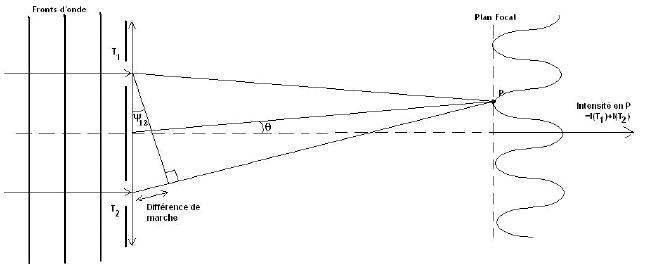
Les astronomes professionnels ont imaginé utiliser le décalage de ces franges et donc la différence de marche entre les rayons du front d’onde, pour remonter à la variation locale du rayon de courbure, et donc obtenir une valeur directe du r0 (Habib & Al 2008). Le système des professionnels utilise un diaphragme a 2 trous intercalé entre l’objectif et le foyer.
L’expression de l’intensité au point M en fonction de x, s’exprime par la relation I(x) suivante. On voit qu’il s’agit d’un sinus cardinal, modulé par une expression en 1+cosinus(Expression+delta(phi)). C’est le cosinus qui représente le comportement des franges d’interférences. L’argument de ce cosinus comprend un terme en delta(phi), terme utile pour la détermination du r0. Si delta(phi) est nul, les franges sont centrées.
 |
 |
 |
Si par contre, les franges ne sont pas centrées sur l’image suivante (delta(phi) différent de 0), cet effet de décalage témoigne d’une variation du rayon de courbure du front d’onde, caractéristique d’une valeur particulière du r0. C’est ainsi que fonctionne l’ISM (interference seeing monitor), mis au point par Habib & Al).
Une analyse comparée des valeurs mesurées par un DIMM et un ISM montrent une très bonne corrélation et la possibilité de faire des mesures directes de r0 via une mesure de franges d’interférence :
 |  |  |
Cette expérience est extrêmement simple à réaliser du point de vue de l’amateur. Elle repose sur l’expérience déjà tentée par Hyppolite Fizeau avec un masque percé de 2 ouvertures placées devant le télescope. Il suffit d’un masque en carton, et d’un télescope, comme nous pouvons le voir sur les photos suivantes.
En utilisant une simple webcam (Toucam Philips) et en patientant jusqu’à ce que la turbulence stagne durant la pose, on obtient des franges d’interférence
 |  |
Aborder la valeur du r0 par les franges d’Young semble à la portée de l’amateur avec un minimum de matériel. Mais il y a probablement encore mieux !
L’expression mathématique de I(x) fait apparaître un terme V devant le cosinus. Ce terme V est appelé « visibilité » des franges. C’est le contraste des franges, qui se défini comme le rapport des intensités suivant :
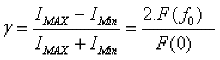
avec I les intensités max et min sur l’image brute et F(f0) l’intensité du pic de la transformée de Fourier de l’image brute.
Ce contraste est égal à 1 pour une source non résolue (ce qui est le cas d’une étoile). Or si nous utilisons une camera posant quelques millisecondes, on constate rapidement que les franges sont translatées, mais aussi que le contraste V est diminué dans l’image de chaque franges de la vidéo :
 |
L’image brute est au centre, les pics latéraux sont les pics de la transformée de Fourier de l’image brute de chaque image. Le contraste V change donc, sur chaque image à temps de pose constant…
L’approche consistant à considérer le contraste d’une source ponctuelle comme toujours égal à 1 (comme dans l’ISM), nous oblige à considérer que les franges sont immobiles pendant la pose. Cette approche n’est jamais réellement le cas, et durant l’exposition de la matrice, les franges sont translatées de manière aléatoire, de part et d’autre d’une position d’équilibre. Elle sont donc « Floutées » par effet de mouvement
Cette visibilité témoigne de la vitesse de fluctuation du tip/tilt pendant la pose, d’où l’idée de mesurer cette vitesse de fluctuation à temps de pose constant.
BLurring Interference Seeing Motion Monitor (BLISMM) :
Flou se traduit par « Blur » en anglais, d’ou l’idée du BLurring Interference Seeing Motion Monitor (BLISMM) On démontre assez facilement, en supposant que le mouvement aléatoire des franges autour de leurs position centrale est une variable aléatoire gaussienne, que le contraste de ces franges C prend la forme suivante : 
avec sigma² la variance de la fluctuation de phase, qui nous permet ensuite de remonter à l’angle balayé par les franges pendant la pose.
La démonstration de cette expression peut être retrouvée de manière exhaustive sur ce lien
 |  |
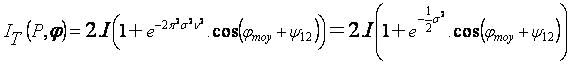
On sait donc, par unité de temps, l’angle balayé par le front d’onde. Connaissant alors la valeur du r0, nous en déduisons l’angle sous tendu par un télescope équivalent de diamètre r0. Nous connaissons la vitesse instantanée a laquelle est balayée cet angle, ce qui nous amène directement à la mesure du temps de tip/tilt tau’0. Regardons expérimentalement ce que cela peut donner :
 |
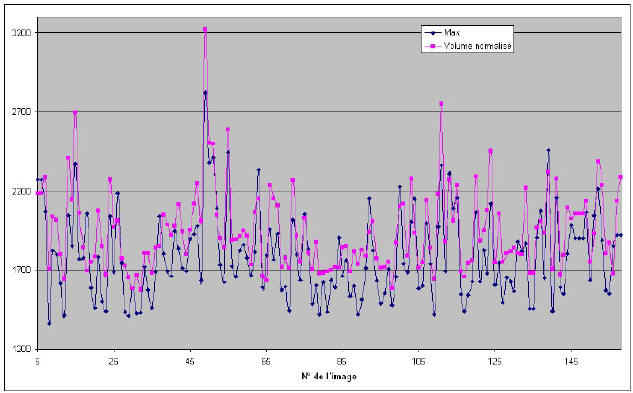
La mesure du contraste des franges sur une séquence video de 150 images permet de se rendre compte de la variabilité de la vitesse de transit des franges pendant la pose. La images de la première ligne de ce tableau nous montre par ordre croissant de contraste, l’aspect des franges extraites (interférogrammes) obtenus sur l’étoile Véga avec une Toucam proII. Les valeurs de contrastes varient ici de 7% à 78%. Nous connaissons donc la variance de phase, sur le temps Tpose, par le contraste des franges. Or t’0 est le temps pour lequel les variations de forme du front d’onde sont inférieure à lambda/2Pi(). Donc si nous connaissons r0, on en déduit epsilon0 et l’on en déduit le temps de cohérence du tip/tilt tau’0 Pour mettre en oeuvre cette mesure en simultané avec celle du r0 et de l’angle d’isoplanétisme théta0, nous avons imaginé un masque d’un type un peu particulier, regroupant les éléments suivants :
 |  |
Le front d’onde incident est prélevé en 3 endroits (trou1, trou2, trou3). On peut remarquer que le diamètre des trous 1 et 3 sont identique de manière à respecter les équations du DIMM. Le problème a été de trouver une pièce optique low cost ayant comme caractéristique de dévier faiblement les rayons collectés par le trou 3 pour effectuer la mesure du r0. Ayant la chance de travailler dans un laboratoire de physique, les physiciens de ce laboratoire m’ont conseillé des plaques de verre synthétique (Polycarbonate de marque LEXAN) dont le défaut moyen de planéité mesuré est de l’ordre de quelques dizaines de microns sur 5cm. On obtient un prisme dont la déviation est de l’ordre de quelques dizaines de secondes. Le spot obtenu est relativement peu dilué et comme on travaille trés haut en focale pour obtenir des franges d’interférences en combinant le flux des trous 1 et 2, la déviation est suffisante pour obtenir un spot exploitable. Donc en occultant séparément les ouvertures, on trouve les configurations suivantes :

|  | Trous 1 + 3 | Trous 1 + 2 |
En résumé donc, si l’on obstrue le trou n°2, nous nous retrouvons dans la configuration d’un DIMM classique (vidéo de gauche). On voit bien que l’information de déplacement différentiel est directement accessible. Les lignes horizontales apparentes sur certaines images de la vidéos sont dues au fait que la matrice CCD de la camera est une matrice interlacée Si l ‘on obstrue le trou n°3, on est dans le cadre de l’expérience de masque de Fizeau, et l’on fabrique alors des franges d’interférences dont le contraste est directement accessible. Donc en procédant a une analyse, sur une séquence vidéo dont chaque image est prise a temps de pose constant (20ms à 25 images/secondes) : – La fluctuation de position différentielle des spots de l’image (dont le centroïde est obtenu en interpolant une gaussienne sur ces spots à chaque images) permettant de remonter à r0 – La mesure du contraste des franges permettant de remonter à tau’0 – La mesure de scintillation par analyse photométrique (en photométrie d’ouverture) du spot issu du trou 3, permettant de remonter à théta0 On obtient les chronogrammes suivants (séquence de 30 secondes, traitements sous Iris) :
 |


epsilon0 et théta0 sont exprimés en secondes d’arc, r0 en millimètres, et tau0 en millisecondes. Le tableau suivant nous montre les statistiques associées aux mesures des 3 quantités évaluées :
 |
Plusieurs séquences vidéos prise montrent des résultats similaires, mais évoluant au cours dela nuit. Il faut garder a l’esprit que les quantités mesurées à chaque images sont des quantités instantanées. Lorsque l’on parle de mesure de seeing, il convient de rappeler que l’angle d’isoplanétisme, le temps de cohérence et le paramètre de Fried n’ont de sens que sur des temps extrêmement courts. Lorsque l’on parle de seeing sur des poses longues, il s’agit de mesures statistiques de ces quantités sur un nombre important de mesures instantanées. On peut alors parler de seeing moyen. Une autre remarque est que l’on constate sur l’analyse des paramètre de la séquence vidéo montrée en exemple, que théta0 varie de manière non corrélées avec r0. Cela veut dire que l’on peut avoir localement, sur l’image d’une étoile, une PSF quasi parfaite (r0 grand), mais qui serait totalement déformée si l’on s’écarte d’un angle petit de la direction de visée (théta0). Réciproquement, on peut avoir un r0 petit (donc une PSF remplie de tavelures), et un théta0 grand (la même structure de tavelures sur un angle de visée grand). Si l’on veut établir, dans l’angle d’isoplanétisme, une sélection des images dont les caractéristiques fréquentielle (finesse des détails) sont les moins entachées d’imperfection, il convient donc de sélectionner les images pour lesquelles le Théta0 est grand, ainsi que le r0, tout en imageant en deça du temps de tip/tilt. Sur la séquence précédente, ces trois conditions sont réunies sur au moins 2 images en fin de séquences (images 564 et 587 si la pose etait réduite a 10ms). Tous cela pour quoi ? Une sélection des images dont la qualité instantanée est maximale est à la base d’une discipline appelée le « Lucky Imaging ».
Le Lucky Imaging:
La définition du Lucky Imaging (Hufnagel 1966 Fried 1974) est la suivante : « -Si les images sont prises suffisament rapidement pour « geler » les mouvements de la turbulence, nous trouvons qu’un nombre significatif d’images sont fines, c’est à dire, que la fluctuation des paramètres statistique (q0, r0 et t0) est minimale. »
-Lucky Imaging Team- University of cambridge- http://www.ast.cam.ac.uk/research/lucky
Une illustration de cette propriété de l’atmosphère est donnée sur l’image suivante :
 | Centre de M13 (Juillet 2007) Telescope 200inches (Palomar) Camera Luckycam (L3CCD) FWHM typique : 35mas |
Nous pouvons voir sur ce champs, deux images affichées en alternance, du centre de l’amas globulaire M13 obtenu au téléscope de 5m du mont Palomar à l’aide d’une camera EMCCD dite LuckyCam. Le champs est suffisament petit pour pouvoir se placer localement dans des conditions d’Isoplanétisme, quand la turbulence le permet. Les deux images sont réalisées à temps de pose constant (et court). L’image floue est une illustration de la dilution des étoiles par les speckles, intégrées le long de la pose, dont le temps de cohérence est visiblement inférieur au temps de pose. Comme nous l’avons vu plus haut, cette valeur du temps de cohérence évolue, ainsi que la valeur du r0. L’autre image, montre au contraire des étoiles fine, dont la largeur à mi-hauteur « FWHM » est typiquement de 0,035 secondes d’arc. Sur cette deuxième image, nous sommes dans le cas ou l’angle d’isoplanétisme est supérieur au champs imagé, le temps de cohérence ne dilue plus l’image (Supérieur au temps de pose) et surtout, le r0 est stable et grand dans la zone d’isoplanétisme !! Sous cette conditions, on obtient des PSF dont la dimension correspond à la limite de diffraction par l’ouverture. Mais cela arrive rarement, d’ou la notion de « Lucky Imaging », c’est a dire imagerie chanceuse. Il faut donc pour réunir ces 3 conditions, sur r0, theta0 et tau0, enregistrer beaucoup d’images et sélectionner uniquement celle remplissant ces 3 critères. Mais l’obtention directe de ces 3 paramètres est, suffisante mais pas forcément nécessaire pour faire la sélection. en tout état de cause, la connaissance du paramètre de FWHM ou du rapport de Strehl dont la figure suivante illustre la définition, permet de remplir un critère de sélection sur les étoiles du patch isoplanétique :

Nous voyons sur cette figure, que le rapport de strehl est le rapport de l’intensité maximale mesurée sur une étoile, sur l’intensité théorique de la tache de diffraction (PSF). Si on normalise l’intensité théorique à 1, hors turbulence, le « strehl ratio » sera de 1, c’est à dire une l’image de l’étoile sera identique à l’image mesurée. En supposant uniquement le déplacement de tilt (1%, 10%, 50% et 100% de l’angle du pic central de la tache d’Airy (PSF)), nous voyons sur l’échelle de gauche, que le strehl ration s’effondre rapidement : 0.7 à 10%, 0.5 à 50%, 0,37 à 100% . Mais le déplacement angulaire peut être plus important encore que la largeur du pic théorique. En moyenne, une monture autoguidée permet d’avoisiner un strehl ratio de 13 à 14%. Ce résultat est important, mais il ne tiens pas compte de l’effet d’étalement de la PSF. Fort heureusement, nous avons vu que pour les diamètres amateurs courants, c’est bien l’effet de tip/tilt qui est prépondérant. Le Strehl ratio et la largeur à mi-hauteur de la PSF sont mathématiquement liées. Comme expérimentalement il est difficile de connaître le maximum du pic théorique d’une étoile du champs pour faire la sélection de la bonne image, les professionnels utilisent plutôt la largeur à mi-hauteur
Dans quels domaines le lucky imaging peut-il être un puissant outils d’imagerie ?
– En imagerie stellaire : Toujours dans l’hypothèse que la sélection s’établi sous condition d’isoplanétisme, la technique la plus employée pour augmenter le rapport signal sur bruit d’une image est celle dite du Shift and Add. La première étape de ce traitement consiste a sélectionner les images dont le strehl ratio est le plus grand. Puis on recale le lot d’images sélectionnée et on les additionne. On retrouve ici des exemples de couples d’étoiles doubles serrées de séparation sub secondes, obtenues par les professionnels de Cambridge sur le télescope NOT de 2,5m de La palma.


(Law&al 2005) Telescope 2,5m (NOT) Camera Luckycam (L3CCD) FWHM typique : 0,12as
Les professionnels ont put remarquer, que la quantité d’images sélectionnées pour l’addition, influait de manière non négligeable sur la FWHM finale du compositage.

Ce tableau montre en abscisse le temps d’exposition (en secondes). En ordonnées, la FWHM mesurée sur le compositage final. Plus cette dernière sera faible, plus l’image sera piquée. Les couleurs respectives des point de mesures montrent sur une même cible, des taux d’acquisitions a différentes vitesses (bleu12Hz, rouge18Hz et vert36 Hz). On constate, avec ces 3 graphes, que plus la sélection est drastique, meilleure est la largeur à mi hauteur des étoiles du champs. A 1% d’images sélectionnées sur une vidéo, on peut obtenir une réduction de la FWHM d’un facteur 3 à 4 (2 à 3 lorsque l’on prend 10% des images), par rapport à la FWHM obtenue en longue pose, sans sélection préalable. Il convient donc, lors d’un compositage, de ne sélectionner qu’une petite partie des images de la vidéo. La question est de savoir sur quel critère se baser pour limiter le nombre d’images d’un compositage en « shift and add ». Nous verrons au paragraphe suivant que la connaissance des paramètres de la turbulence permet de restreindre le nombre d’images selon une loi bien connue des professionnels
Au niveau amateur, la série d’image suivante montre bien la possibilité, avec un télescope de diamètre modeste (ici 300mm), l’intérêt de la méthode de sélection de type lucky imaging, et ce en fonction de la bande spectrale dans laquelle est obtenue l’image.

L’étoile imagée ici à une séparation de 0,56″ d’arc. Une sélection de 30 images seulement sur quelques centaines de chaque vidéos permet de résoudre sans trop de soucis ce couple d’étoiles doubles. L’avantage de cette méthode sur l’interférométrie des tavelures, est qu’il n’y a pas de limite sur l’écart de magnitude entre les composantes du couple. Sa limitation, par contre, est qu’elle est applicable uniquement sous condition d’isoplanétisme (dans l’angle sous tendu par théta0).
– En imagerie planétaire : D. L. Fried démontra en 1977que la probabilité d’obtenir, sur une séquence d’image à court temps de pose, une image respectant un critère de déformation du front d’onde lambda/(2Pi) (c’est à dire respectant le critère définissant la rayon de Fried), s’exprimait en fonction du rapport du diamètre de la pupille d’entrée sur le r0 sous la forme suivante :
 pour D/r0>3.5
pour D/r0>3.5



En 2005, Cyril Cavadore utilisait cette relation pour obtenir l’abaque présentée ci dessus, en fonction de différents diamètres de pupille. On y voit clairement que la probabilité d’obtenir une bonne image avec un r0 de 60mm est de 1 pour une pupille de 200mm. Cela chute a une image sur 10 pour une pupille de 305mm, et une image sur 10000 pour un 500mm ! La connaissance du r0 moyen au cours de l’acquisition d’une séquence vidéo planétaire permet d’estimer la probabilité d’obtenir une image de bonne qualité mais il ne s’agit que d’une probabilité et non d’une statistique. Pour comprendre la subtilité, si nous considérons un dé a 6 façes, nous savons que la probabilité est de 1/6 pour obtenir le chiffre que l’on souhaite. Mais il peut arriver que sur 10 tirages, on obtienne 5 fois le chiffre 6 et sur 10 autres tirages on en l’obtienne pas du tout. Il faut donc, pour se rapprocher au mieux des conditions de cette loi de probabilité, emmagasiner le maximum d’images, et se restreindre, via la connaissance du r0, au nombre d’images à compositer correspondant à ce que nous propose la probabilité de Fried. Au niveau amateur, la limitation principale, comme le montre brillamment Christian Viladrich [18] en imagerie solaire, reste que le critère de probabilité de Fried n’est valable que dans la zone d’isoplanétisme. Nous pouvons voir d’ailleurs sur le tableau précédent, que le cliché de droite correspondant à une registration effectuée à l’aide du logiciel Registax, laisse apparaître des zones légèrement floues sur les bord de l’image, dues au défaut d’isoplanétisme. La notion de lucky imaging en imagerie planétaire doit donc tenir de la probabilité locale d’avoir simultanément un angle théta0 grand, et au sein de chacune des zones isoplanétiques, un r0 grand pour respecter le minimum de déformation de l’image espéré. Des approches professionnelles commencent a voir le jour ([19] Zhu&Al 2013) pour permettre d’établir une sélection de type lucky imaging par zone, et reconstituer une image en recollant les patch isoplanétiques de meilleure qualité. Un logiciel amateur de type Autostakkert utilise a l’heure actuelle une approche similaire et donne des résultats extrêmement probant sur des surfaces planétaires de grande dimensions angulaires (plusieurs minutes d’arc). Si l’objet est toutefois de petites dimension, on peut reste dans un mode de sélection des images respectant la condition d’isoplanétisme et sélection par lucky imaging, comme montré dans l’exemple suivant sur le satellite galiléen Io :

Cette image, obtenue sur une série de 4000, correspond à la combinaison des 3 facteurs respectant les conditions du Lucky Imaging, à savoir théta0 grand, r0 grand (mesuré par la probabilité de Fried sur l’ensemble de la séquence : 78mm), et un temps d’exposition court (
Io à la date de la prise de vue présentait un diamètre apparent de 0.9 secondes d’arc. Le tableau suivant regroupe une simulation des détails présents à la surface de Io au moment de la prise de vue, les trois images sélectionnées sur l’ensemble de la séquence :
Aucun traitement n’a été effectué sur ces images, juste un resserrage des seuils de visualisation. Il est difficile de conclure directement sur les détails les plus fins (avoisinants les 0,3″ donc la limite théorique d’un 600mm), mais au demeurant, on peut toutefois noter une zone claire sur la partie inférieure gauche du satellite, et la présence d’un détail sombre sur la partie supérieure droite, qui correspond aux détails de la simulation. On peut noter aussi que ces 3 images ne sont pas consécutives au sein de la séquence vidéo acquise.
Nous avons vu au cours de ces quelques lignes, les définitions principales des paramètres qualifiant la turbulence atmosphérique, et dont l’utilisation abusive dans certains cas, peut conduire en astronomie amateur, à ne pas forcément comprendre quels phénomènes amènent à la dégradation des images de nos installations. Et encore, je me suis ici limité à la turbulence atmosphériques, j’enjoint le lecteur à se reporter en particulier à la référence [18] (C. Viladrich), détaillant en particulier la turbulence instrumentale, cause de dégradations qui n’ont pas été abordées ici.
Nous avons dégagé un moyen simple permettant avec des moyens accessibles aux amateurs, de faire une mesure des paramètres Théta0, Tau’0 et r0 qui combinés, nous donnent une statistique vraie sur l’état de la turbulence dans une direction d’observation donnée.
Toutes ces considérations sur la mesure de la qualité de la turbulence, sont destinées au final à mettre en oeuvre la technique du « Lucky Imaging » et à rechercher, sur des séquences vidéos faites avec des caméras amateurs, les images qui respectent au mieux les critères de qualité définis par Tau’0, Théta0 et r0
On peut, de ces mesures, dégager des points essentiels :
1 – La connaissance de Tau’0 (détermination du temps de cohérence de la turbulence) permet de définir un temps de pose optimal en dessous duquel les images ne seront pas trop « floutées »
2 – La détermination de Théta0 par la fluctuation de scintillation permet de sélectionner les images ou la turbulence est homogène
3 – La détermination, de r0 à chaque pose, en dernier lieu devient l’un des 2 critères (voir plus bas) pour sélectionner les images ou la turbulence est minimale
Sous ces trois conditions, il convient d’approcher la notion de lucky imaging de manière spécifique en fonction de l’objet imagé :
En fonction de l’objet cible, il faut choisir des cameras adaptées :
– En planétaire, ou le flux reste important = Basler ou autre ayant un débit de plus de 100ips pour passer sous le temps de cohérence.
– En ciel profond ou le critère le plus important sera le très faible flux de la source, suivi par le temps de pose court, d’ou la nécessité d’une camera EMCCD…
2 – Mesure de l’indice de scintillation de la source pour être sur du Théta0 par image et trigger la camera
3 – Détermination de r0 à chaque pose (ou mesure de FWHM courte pose d’une étoile du champs si l’on travaille en ciel profond)
[1] M. FRANCON, S. SLANSKI « Cohérence en optique » 1965, Éditions du CNRS
[2] F. RODDIER, P. LENA « Long-baseline Michelson interferometery with large ground-based telescopes operating at optical wavelength I » 1984, Journal of optics (Paris) Vol 15, n°4. pp. 171-182
[3] C. RODDIER, F. RODDIER « Interferogram analysis using Fourier transform techniques » 1987, Applied optics, Vol 26, n°9 p1668-1673
[4] D.L. FRIED « Limiting resolution looking down through the atmosphère » 1966, Journal of the optical society of america, Vol 56 n°10 pp. 1380-1384
[5] F. RODDIER « Les effets de la turbulence atmosphérique sur la formation des images visibles et infrarouges » 1979, Journal of optics (Paris) Vol 10, n°6, pp.299-303
[6] D.L. FRIED « Optical resolution through a randomly inhomogeneous medium for very long and very short exposures » 1965, Journal of the optical society of america, Vol 56 n°10 pp. 1372-1379
[7] D.L. FRIED « Statistic of a geometric representation of wavefront distortion » 1965, Journal of the optical society of america, Vol 55 n°11 pp. 1427-1435
[8] J. VERNIN, C. MUÑOZ-TUÑON « Measuring astronomical seeing: the DA/IAC DIMM » 1995, Publication of the astronomical society of pacific 107, pp. 265-272
[9] D. BONNEAU « Expérience acquise en interférométrie optique à 2 télescopes » 1979, Journal of optics (Paris) Vol 10, n°6, pp.311-316
[10] R HANDBURRY BROWN « The Intensity Interferometer » 1974, Taylor & Francis Ltd
[11] C.RODDIER, F. RODDIER « Seeing effect removal in a Michelson Interferometer » 1976, J. Opt. Soc. Am., vol. 66, n°12, December
[12] F. D. EATON and Al, « Isoplanetic angle direct measurments and associated atmospheric conditions » 1985, Applied Optics, Vol. 24, n°19, October
[13] J. KRAUSE-POLSTROFF and Al, « Instrument comparison : corrected stellar scintillometer versus isoplanometer » 1993, Applied Optics, Vol. 32, n°21, July
[14] G.C. LOSS, C. B. HOGGE, « Turbulence of the upper atmosphere and isoplanetism »1979, Applied Optics, Vol. 18, n°15, August
[15] A. TOKOVININ, « Turbulence profiles from the scintillation of stars, planets and moon » 2007, Workshop on Astronomical Site Evaluation, RevMexAA, 31, 61-70
[16] D.L.FRIED « Probability of getting a lucky short-exposure image through turbulence » 1978,Journal of the optical society of america, Vol 68 n°12 pp. 1651-1658
[17] M. SARAZIN, F. RODDIER « The ESO differential image motion monitor » 1990, Astronomy & Astrophysics. 227, 294-300
[18] C. VILADRICH « Turbulence et Seeing » 2012, Rencontres du Ciel et de L’espace Octobre 2012
[19] X. ZHU, P. MILANFAR « Removing Atmospheric Turbulence via Space-Invariant Deconvolution » 2013, IEEE Transaction on pattern analysis and machine intelligence, Vol 35, N°1, January 2013




Conclusion
Bibliographie


