Première version de masque pour SC8″

La première approche des fanges d’interférence peut se faire de la manière la plus simple possible, avec un masque en carton placé devant le télescope. Cette simple approche permet déjà de se rendre compte du phénomène

Deux ouvertures placées de part et d’autres du miroir secondaire et un grossissement permettant de détailler la tache d’Airy sont deux conditions suffisantes pour faire apparaître en visuel sur une étoile brillante des franges d’interférences. L’image (datant des années 2000) précédente montre le montage simplissime à mettre en œuvre. Cela peut être fait par exemple à l’occasion d’une Star Party comme ce fut le cas de manière totalement improvisée en 2019 lors des RAAGSO à l’aide d’un carton découpé mis en place sur le télescope de 400mm de Gérard Arlic (que je salue au passage).

Pour vérifier la présence de franges, il suffit de masquer l’une des deux ouvertures pour les faire disparaitre. L’effet a quelque chose de saisissant

La première image de franges que j’ai obtenu en imagerie est une image obtenue sur Sirius, à l’aide d’un masque un peu plus évolué que le masque en carton. En effet, la caractéristiques de ces franges dépendent de l’écartement des trous, et les équations de visibilités de ces franges dépendent justement de la taille de la source et de la distance entre les trous. C’est pourquoi j’ai conçu et réalisé un premier prototype de masque à distance variable entre les trous.

C8 oculaire 10 mm Camera CB245. Soft : Win245 Temps d’exposition 750ms. Écartement des fentes 165mm, Largeur de fentes 30mm. Image obtenue en 1999.

L’image est brute, juste une soustraction d’offset et un seuillage.

Quelques détails sur l’engin qui permet d’obtenir ces franges. Il s’agit d’un « capuchon », constitué de deux rondelles de CP de 22mm (diamètre 270mm) serrées entre elles par trois vis à 120°. La rondelle inférieure est percée d’un trou dont le diamètre intérieur est au diamètre extérieur du tube d’un C8. Sa marche aussi sur un LX200.

Masque à trous à écartement variable

La rondelle supérieure est percée de deux trous rectangulaires de 50mm par 70mm. Sur ce cache, est fixé un rectangle constitué de deux morceaux de cornière en alu (en U), et deux pièces de liaison en alu plein servant de support au système d’entraînement. Les cornières sont utilisées pour assurer le guidage des deux fentes dans le plan du front d’onde incident (autrement dit, dans un plan perpendiculaire à l’axe optique), à l’aide de cales en teflon. Les deux fentes sont des plaques d’alu de 5mm d’épaisseur, dont les fentes sont fraisées ensembles de manière à avoir rigoureusement les mêmes dimensions. Le guidage le long du diamètre est assuré par un rail de chariot d’imprimante matricielle et deux chariots d’imprimantes de récupération (Merci à Philippe Dupouy, et à l’observatoire de Dax). Les paliers de ce type de rails semblent être en bronze, ce qui assure un frottement très doux et surtout parfaitement rectiligne. Toujours récupérés sur une imprimante, des poulies d’entraînement de chariot et le câble allant avec, assurent le déplacement symétriques des deux fentes. Lorsque le câble inférieur, accroché sur la fente inférieure droite se déplace, la partie supérieure gauche du câble fixées sur la deuxième fente (en haut à gauche) se déplace en sens opposé. Les deux fentes ont donc toujours un déplacement de sens opposé. Il aurais été plus facile d’utiliser un système à double crémaillère, mais ces pièces mécaniques sont plus délicates a trouver.

Le système d’entraînement et de mesure est un micromètre récupéré sur un spectro de laboratoire (j’ai gardé les pièces pour faire de la spectro un jour ;-)). Ce type de micromètre est un simple Palmer, mais dont la particularité est de pouvoir être entraîné par un pignon. D’où l’envie de motoriser l’ensemble pour éviter de faire vibrer le télescope pendant qu’on observe les franges. L’isolation lumineuse des trous du cache est assurée par un soufflet de canson noir (je pense qu’il faudra le changer régulièrement à cause de l’humidité).

L’ensemble s’alimente sous 12 V, et est quasi exempt de vibrations. On devrais donc maintenant voir disparaître les franges en restant tranquillement derrière l’oculaire.

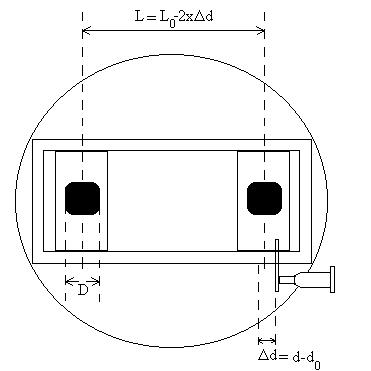
La source étalon utilisée cette fois ci fut Altair, magnitude 0,8.Les conditions de prise de vue sont les suivantes :LX200 8″ f/D: 10 Oculaire Pössl 12,5mm + tirage 80mm. Caméra Audine Tps d’exposition 0,1 s, bin 1×1, Maskatrou V1. Traitement d’image sous IRIS (C. Buil). Acquisition de séries de 50 poses, sélection manuelle des 10 images comportant les franges les plus évidentes, puis analyse des pics à la fréquence f0 obtenues sur la FFT (transformée de Fourier) directe de chacune des images afin d’obtenir celle comportant le meilleur contraste. Pour mémoire, nous rappelons ici la géométrie du maskatrou V1 pour comprendre la détermination de la longueur L séparant le centre des deux fenêtres d’entrée.

Le tableau suivant regroupe les images sélectionnées, pour chaque écartement, ainsi que la FFT équivalente, les statistiques obtenues sur les pics à la fréquence f0 sur une fenêtre de dimension constante, ainsi que la valeur estimée manuellement du centre du pic (en effet, les FFT obtenues comportant le long de l’axe vertical une ligne quasi continue du aux effets de bord, les valeurs statistiques ne donnent pas la position exacte du maximum du pic f0 du point de vue géométrique.

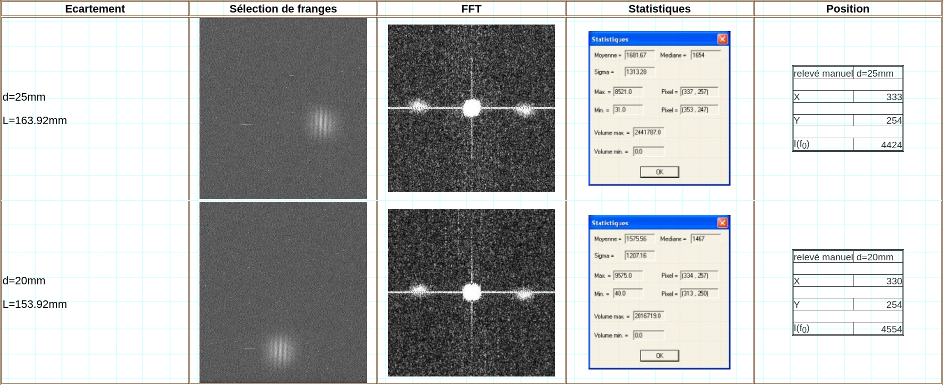
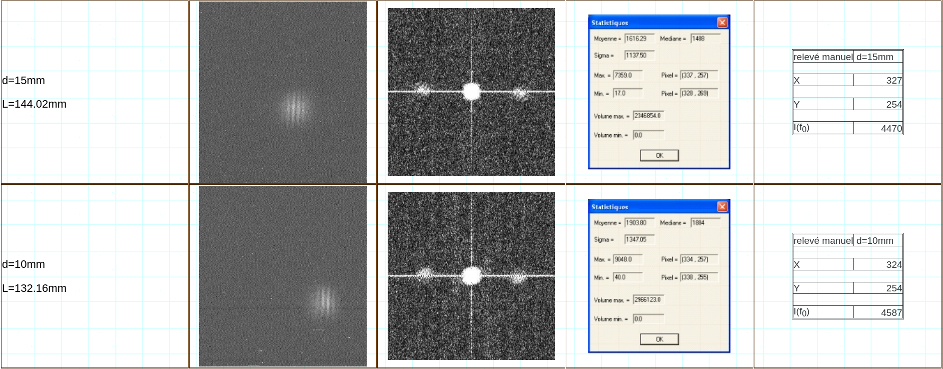
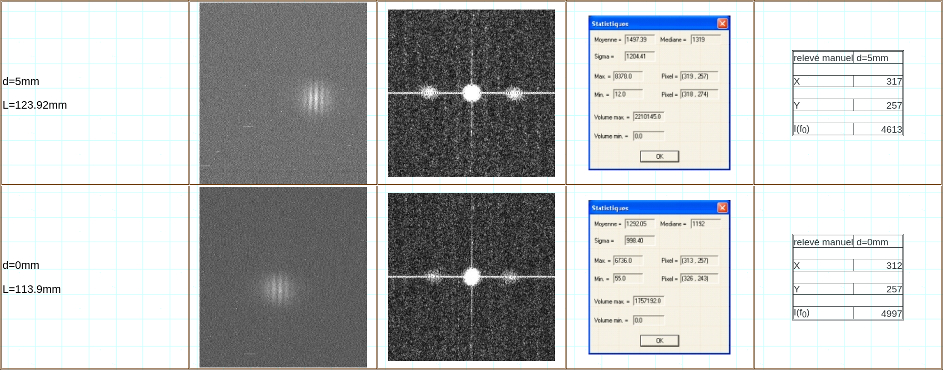
Nous obtenons donc l’évolution de la position de pic à la fréquence f0 fonction de la valeur de L en écrivant R la distance au centre de la FFT, ce qui traduit un retrécissement des franges, ce qui tombe bien car c’est justement ce que nous appprend la théorie !

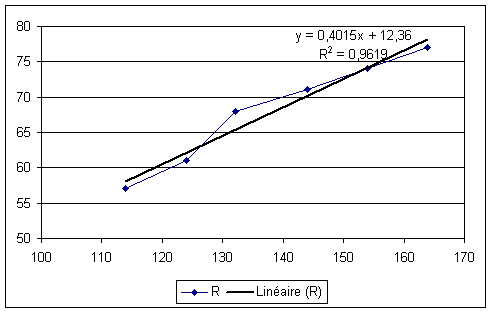
Nous avons donc dans cette configuration optique une augmentation de la distance au centre de la FFT d’environ 0.4 pixels par mm d’écartement. Ceci montre qu’au niveau précision sur la longueur L, une précision à 5mm est amplement suffisante pour prévoir la position du pic de lecture.

Quand est-t-il de la valeur du contraste absolu mesuré…. Les fluctuations de valeurs des maximums est inférieure à 4% autour d’une valeur de 91%… C’est encourageant.

Résolution d’une source artificielle :

Etape suivante, tenter de résoudre une source artificielle dont la taille angulaire soit dans la fourchette des angles accessibles a l’aide de ce masque.

La source utilisée est un spot rouge avec une fente constituée de deux lames de rasoirs. La largeur de la fente est de 50 microns (mesurée sous microscope). Cette source est placée à 12m70 du telescope ce qui nous donne un angle de 0.81″ d’arc.

Le système de prise de vue est un C8, avec le masque à trous présenté précédemment, plus une barlow, et une camera PC464 VC Phillips ports USB (comme quoi ont peut faire un peu d’interfero avec des webcams).

L’image de droite est l’image de diffraction par la fente, après passage dans un seul des deux trous du masque. On peut remarquer sur les lobes de diffraction secondaires (au dessus et au dessous de l’image de la fente), que la coloration est différente lorsque l’on s’éloigne du maximum (rouge vers le centre, bleu vers l’extérieur du lobe). Sur l’image de gauche, les deux ouvertures du MTR ne sont pas obstruées. on voit alors apparaître dans le lobe principal de diffraction, les franges tant attendues. Dernière chose, la providentielle augmentation de luminosité faisant apparaître les lobes de diffractions vient du filament du spot, juste derrière la fente. Nous mettons aussi ici en évidence un problème quand à la prise de vue. En effet, nous sommes ici en limite de sous échantillonnage, puisque les franges sombres et claires sont échantillonnées aux environs d’un pixel par frange. Sachant que d’après la littérature, il est souhaitable d’échantillonner aux environs de deux pixels par franges pour obtenir des résultats exploitables.

Une chose importante à vérifier est aussi la variation d’angle des trous par rapport à l’axe de symétrie de la fente. La rotation

Sensibilité de la visibilité des franges à l’orientation du masque par rapport à l’orientation de la source.La fente est verticale, et la camera est perpendiculaires aux franges. Image de gauche, le MTR fait un angle de 20° avec l’horizontale, celle du milieu 10° et celle de droite 0°. Le contraste des franges est donc une fonction de l’angle source/axe des trous

Tachons maintenant de résoudre la source en variant l’écartement des trous. Le contraste des fanges correspond à la mesure de al différence de niveau entre la frange brillante centrale, et les franges sombres contigue à la frange centrale. Les valeurs sont directement extraites sous Iris de C. Buil

Image de gauche, écartement 126mm contraste mesuré : 34,33%

Image du milieu, écartement 144mm contraste mesuré : 28,96%

Image de droite, écartement 164mm contraste mesuré : 8,21%

Pour l’image de droite, la source est quasi résolue (on voit encore quelques résidus de franges en s’approchant du filament de l’ampoule).

Essayons de quantifier la taille de cette source. La courbe de contraste étalon d’ouverture circulaire correspond à une fonction de Bessel du premier ordre, mais ici les ouvertures sont carrées, on peut trouver dans les cours d’optique disponible sur l’internet, le profil d’extinction qu’il convient d’utiliser dans le cadre du masque que nous utilisons.Ici, il s’agit d’un simple Sinus Cardinal (f(x)=Sin(x)/x). La source présente sur l’axe une dimension théorique de 0,812″ d’arc. La courbe étalon à utiliser pour obtenir la valeur de la première extinction est alors la suivante :

Nous obtenons alors 3 points correspondant à des valeurs de Z, pour lesquelles B (l’écartement des deux ouvertures), est connu. L’extinction des franges intervient pour une certaine valeur de B, au moment ou la source est résolue. Nous n’avons pas atteint cette valeur, mais nous disposons d’une relation linéaire entre Z et B qui nous permet d’obtenir la valeur de B pour laquelle le contraste s’annule. Ceci intervient pour Z=Pi ce qui nous donne une extinction pour B=181,8mm. Cette valeur est obtenue grâce à une régression linéaire sur les 3 points de mesure :

La formule permettant alors d’obtenir l’angle sous tendu par la source est alors :

Soit avec l=0,65mm, puisque le max d’émission du spot se situe vers le rouge, on obtient f=0,74″ d’arc.

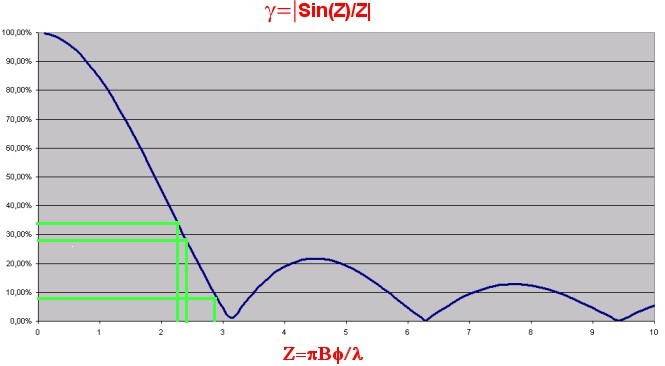
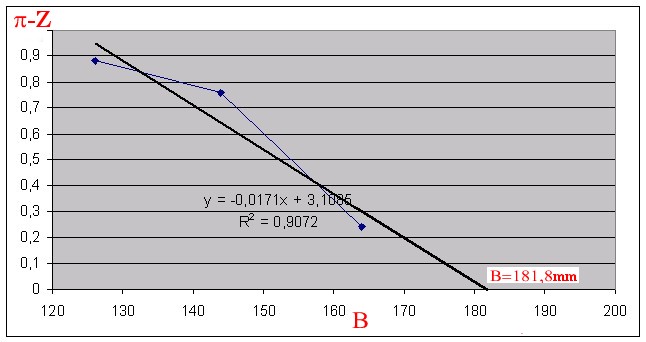
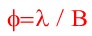
Quelle est la validité de cette mesure (attention, je ne vais pas encore faire un calcul d’incertitude….). Eh bien sachant que la source est a 12m70 à +/- 1cm, cela correspond à une taille de fente de 45,4mm (faites le calcul ;-)).

Si l’on se rappelle que la source à été mesurée au microscope optique à 50mm avec une incertitude de 2mm, on tombe au dessous de 9% d’erreurs sur la mesure de l’angle, soit environ sept centième de seconde d’arc. Plutôt intéressant.

En étant parfaitement optimiste, je pourrais dire qu’une bonne partie de l’erreur tient au fait que la fente était tenue par du scotch sur le spot, et qu’elle n’était pas rigoureusement dans l’axe ( 25° d’inclinaison sur l’axe suffiraient à expliquer 5mm d’écart sur la mesure), alors pourquoi pas ??

Nous avons donc avec cette petite manip de labo, réussi à mesurer une source ayant la taille d’un quart de cheveu à une distance de 12,7 mètres (ce qui illustre bien l’expression couper les cheveux en 4).

Conclusion

Le masque que nous avons employé ici, fonctionne donc parfaitement dans la plages des valeurs d’angles proche de la résolution théorique du télescope servant de combineur (le C8 utilisé pour l’expérience). Toutefois cette fourchette d’angle que l’on peut résoudre, dépendant d’un écartement des trous allant de 120 à 160mm, laisse une marge faible dans la quantité d’objet d’intérêt que l’on pourrait mesurer à l’aide de cette technique. De plus, la faible surfaçe des trous d’entrée ne permet pas d’atteindre des magnitudes très basses au regard du besoin pour la génération des franges.

Ce masque de petite dimension constitue en fait une approche pédagogique de la mesure de contraste de frange, un TP utile pour comprendre et mettre en oeuvre la manip. Toutefois, des mesures directes peuvent être envisagées avec un télescope de plus grand diamètre, ainsi que des ouvertures de plus grande dimensions, comme nous pouvons le voir sur la page suivante consacrée aux masques de Fizeau