Sommaire
Résumé : La difficulté de réalisation pratique d’un interféromètre stellaire de type Fizeau-Michelson (pupille diluée) avec des moyens amateurs, tiens à l’extrême précision requise dans les chemins optiques que doit parcourir la lumière issue de l’étoile jusqu’au capteur destiné à recevoir l’image des interférences. Cet article décrit la première réalisation par un amateur d’un interféromètre de type Fizeau-Michelson, permettant de faire interférer les faisceaux lumineux prélevés au-delà du diamètre du télescope au moyen d’un système optique périscopique. Pour y parvenir, une ligne à retard optique intégrée dans une oculaire à été mise au point. Des franges d’interférences ont été obtenues sur Bételgeuse et Sirius

Introduction
L’observation astronomique en interférométrie optique est un domaine réputé difficile et délicat, à tel point que peu d’astronomes amateurs ont tenté de s’intéresser au sujet. Trois domaines principaux de cette technique observationnelle peuvent être distingués : l’interférométrie des tavelures, permettant de « restaurer » le pouvoir résolvant d’un télescope dont les images sont perturbées par la turbulence atmosphérique, l’interférométrie de recombinaison via un masque comportant deux ouvertures, ce que l’on peut qualifier de masque de Fizeau-Stephan, consistant à combiner la lumière passant par 2 trajets optiques distinct, pouvant être simplement deux ouvertures devant le télescope. La troisième catégorie de techniques est celle de l’interférométrie à pupille diluée comme l’interféromètre de Fizeau-Michelson à poutre optique périscopique ou l’interféromètre à télescopes indépendants inventé par Labeyrie. Ces deux derniers systèmes permettent d’accéder à des domaines de résolution au-delà du diamètre d’un télescope seul. Dans ce type d’interféromètre, la résolution angulaire est limitée par la distance B des ouvertures à λ/B >> λ/D avec D le diamètre d’un télescope seul. Or la métrologie des longueurs de chemins optique dans ce domaine de l’interférométrie de recombinaison, occupe une place prépondérante. Toute la difficulté consiste en l’ajustement des longueurs de chemins optiques avec une précision de l’ordre de la longueur d’onde des photons issus de l’étoile. Mais pour bien comprendre comment ces propriétés sont apparues à l’esprit humain, il est nécessaire de faire un petit retour en arrière sur l’histoire de la découverte des phénomènes d’interférences lumineuses, leur nature physique, ainsi que sur leur propriétés, dont nous pouvons tirer profit en astronomie pour obtenir des mesures caractéristiques de la source émettrice de cette onde, et tout particulièrement sur les dimensions des étoiles simples, ou sur la séparation des étoiles doubles.
Historique
Du point de vue historique, les propriétés ondulatoires de la lumière, ont été mises en évidence par l’Anglais Thomas Young au tout début du XIXème siècle. Cette époque fut le début d’une révolution conceptuelle sur la nature de la lumière qui, depuis Newton, était considérée comme constituée de corpuscules, autrement dit des particules se déplaçant en ligne droite, et doté d’une énergie cinétique. Malheureusement pour Sir Isaac Newton, sa théorie corpusculaire n’expliquait pas certains phénomènes lumineux tels les phénomènes de diffraction, de polarisation ainsi que les phénomène d’interférences lumineuses. C’est en 1801 que Sir Thomas Young dans sa célèbre expérience dite « des trous d’Young » démontre le caractère ondulatoire de la lumière et étudie les propriétés des franges d’interférences. Quelques années plus tard, le Français Augustin Fresnel établi le cadre théorique de ces premières expériences, et François Arago montre au travers de ses expériences sur la diffraction, l’importance de la dimension angulaire de la source dans la genèse des phénomènes particuliers que sont les interférences et la diffraction (tache de Fresnel) en optique ondulatoire. Mesurer la dimension angulaire d’une source deviens donc possible en étudiant l’intensité des phénomènes ondulatoires associés. Un télescope n’étant qu’un système de grandissement optique, la mesure de la visibilité des franges d’interférences dans le télescope deviennent alors le moyen d’obtenir une information sur la dimension de la source qui leur a donné naissance. Ces propriétés particulières des franges d’interférences ont poussé Hippolyte Fizeau, aux environs de 1850, à envisager de mesurer la séparation d’étoiles doubles serrées, ainsi que d’estimer le diamètre d’étoiles simples, mais c’est Édouard Stéphan qui à l’observatoire de Marseille, utilisa cette méthode le premier, sur un télescope de 80cm, à l’aide d’un masque portant 2 « lunules » séparées de 65cm. L’observation de l’absence de chute du contraste des franges par E. Stéphan de l’ensemble des étoiles de magnitude inférieure à 4 lui a permis de conclure à une limite haute des dimensions angulaires d’étoiles brillantes à 0,158’’ de degrés. (Pour de plus amples informations, se reporter à l’excellent article de la Revue L’astronomie juillet/aout 2014 vol 128 p 74 « la mesure interférométrique des diamètres stellaires » D. Bonneau) C’est, dans une correspondance entre Fizeau et Stephan en 1851 que l’on peut retrouver une idée de mise en œuvre d’une méthode de dépassement de la limite imposée par le diamètre du miroir primaire du télescope servant à générer les franges d’interférence (Figure 7). Dans ce schéma de principe, Fizeau suggère de prélever l’onde incidente de part et d’autres du miroir du télescope à l’aide d’un système de deux périscopes, et ce afin d’augmenter la largeur de base, donc la résolution accessible par un télescope donné..
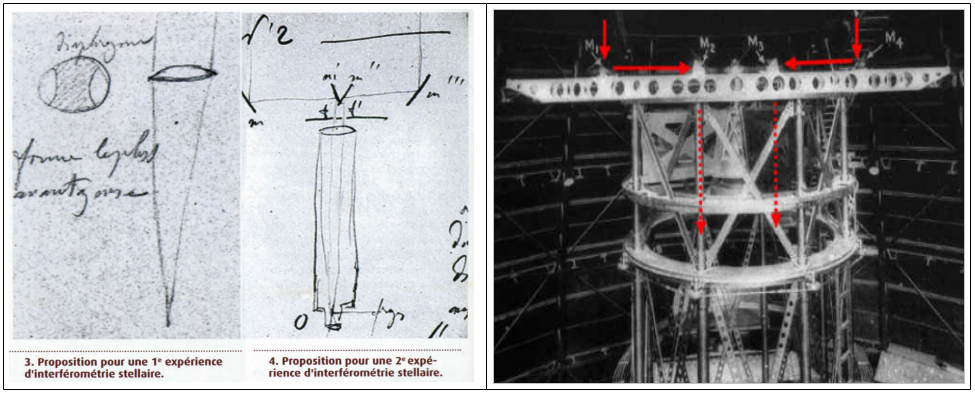
Il fallut attendre 70 ans avant que la mise en œuvre du principe de la poutre périscopique de 6m installée sur le télescope de 2,5m du mont Wilson, permette à Abraham Michelson de mesurer pour la première fois un diamètre stellaire, celui de l’étoile Bételgeuse. Le principe de la poutre de Fizeau/Michelson conduit donc à « dépasser » le pouvoir résolvant d’un télescope en recombinant deux faisceaux incidents au-delà du diamètre du miroir primaire, ce dernier ne servant au final qu’à la recombinaison de ces deux faisceaux en générant les franges d’interférences. La contrainte majeure d’un tel système travaillant en lumière blanche, réside dans la précision des longueurs de chemin optique nécessaire à la recombinaison des deux faisceaux. En effet, les deux faisceaux doivent se combiner, pour former les franges d’interférences, en ayant parcouru un trajet identique à la fraction de longueur d’onde près.
Principe physique des interférences
Pour bien comprendre le principe physique sous-jacent aux mesures que l’on peut faire en interférométrie de recombinaison, il faut revenir aux principes physiques découvert au début du XIXème siècle. L’expérience des trous d’Young peut se résumer de manière extrêmement simple, puisqu’elle consiste à faire interférer (d’où le terme d’interférence) deux faisceaux lumineux issus d’une même source.
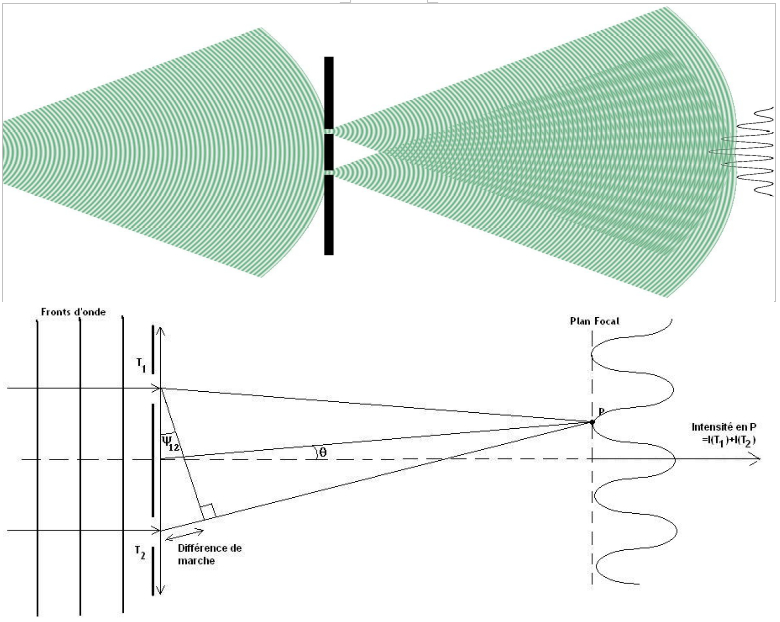
En supposant une source ponctuelle (ou considérée comme telle car située à l’infini), émettant une onde lumineuse à une longueur d’onde donnée, si nous interposons sur le trajet de cette onde lumineuse un écran percé de deux ouvertures dont les dimensions sont proches de la longueur d’onde, chaque ouverture se comportera alors comme une source propre (principe optique de Huygens-Fresnel) dont la fréquence est celle de la source, et dont les battements sont synchronisés (ont dit aussi en « phase »). Au delà de l’écran, les deux ondes vont donc se propager et s’additionner en tout points, mais si par cas un maximum de l’une des ondes correspond au maximum de l’autre en un point particulier de l’espace, alors les intensités des deux ondes s’additionnent et en ce point l’intensité que l’on pourra mesurer sera le double de l’intensité de la source. A contrario, si un maximum de l’une des ondes correspond au minimum de l’autre en un point particulier de l’espace, alors les deux ondes s’annulent en ce point (Figure 1). Ainsi si l’on dispose un écran parallèle au plan des deux ouvertures, on pourra y voir figurer une succession de valeurs d’intensités de l’onde résultante oscillant entre 0 et deux fois la valeur de l’onde incidente. Cette succession de maximums et de minimums de l’onde, dans un référentiel lié à l’axe optique pris comme référence et perpendiculaire aux deux ouvertures, est caractérisé par ce que l’on appelle la Différence de Marche (ddm). Cette notion nous sera essentielle pour la suite. Si maintenant nous interposons un télescope (système de grandissement optique) entre l’écran percé de deux trous, et l’écran collecteur placé au foyer de ce dernier, nous nous affranchissons de la condition précédente, selon laquelle la taille des ouvertures devait être de l’ordre de la longueur d’onde. Le mélange entre les deux ondes se fait dans le plan focal du télescope, et la succession des franges se fait avec un différence de marche de lambda/B avec lambda la longueur d’onde de l’onde incidente, et B la distance entre les deux trous du masque.

L’image présentée sur la Figure 2 est celle de l’étoile Capella, obtenue avec un temps de pose de 20ms et une caméra WATEC 902H2 très courante dans le domaine de l’observation des occultations d’étoiles par des astéroïdes. Cette expérience extrêmement simple à réaliser puisqu’il suffit de poser un masque à deux ouvertures devant le télescope été réalisée, entre autres, au cours de la réunion de la commission des étoiles doubles de la Société Astronomique de France, ou les participants ont pu par eux même, constater la simplicité de mise en œuvre de ce phénomène physique (Figure 4).

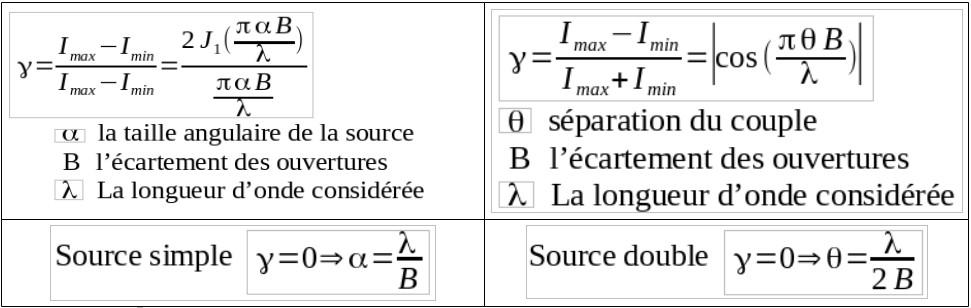
Ce phénomène d’interférence présente un intérêt particulier, car on peut démontrer que le contraste des franges est directement liées à la taille de la source qui leur a donné naissance. En effet, si l’étoile ne se présente plus à l’entrée dans le télescope comme un point non résolu, mais bel et bien comme un disque, elle peut être considérée comme composée d’une multitude de sources individuelles ayant des caractéristiques (longueur d’onde et phase) différente de sa voisine. La cohérence de la source n’est plus assurée et le contraste des franges va alors diminuer. Nous pouvons démontrer mathématique-ment que ce contraste des franges d’interférences (Figure 4), dépend directement de la taille de la source, si l’on suppose cette dernière comme étant celle d’un disque de brillance uniforme ou comme la superposition de deux sources ponctuelles (étoile double) de séparation et d’angle connu par rapport à l’horizontale (Figure 5).
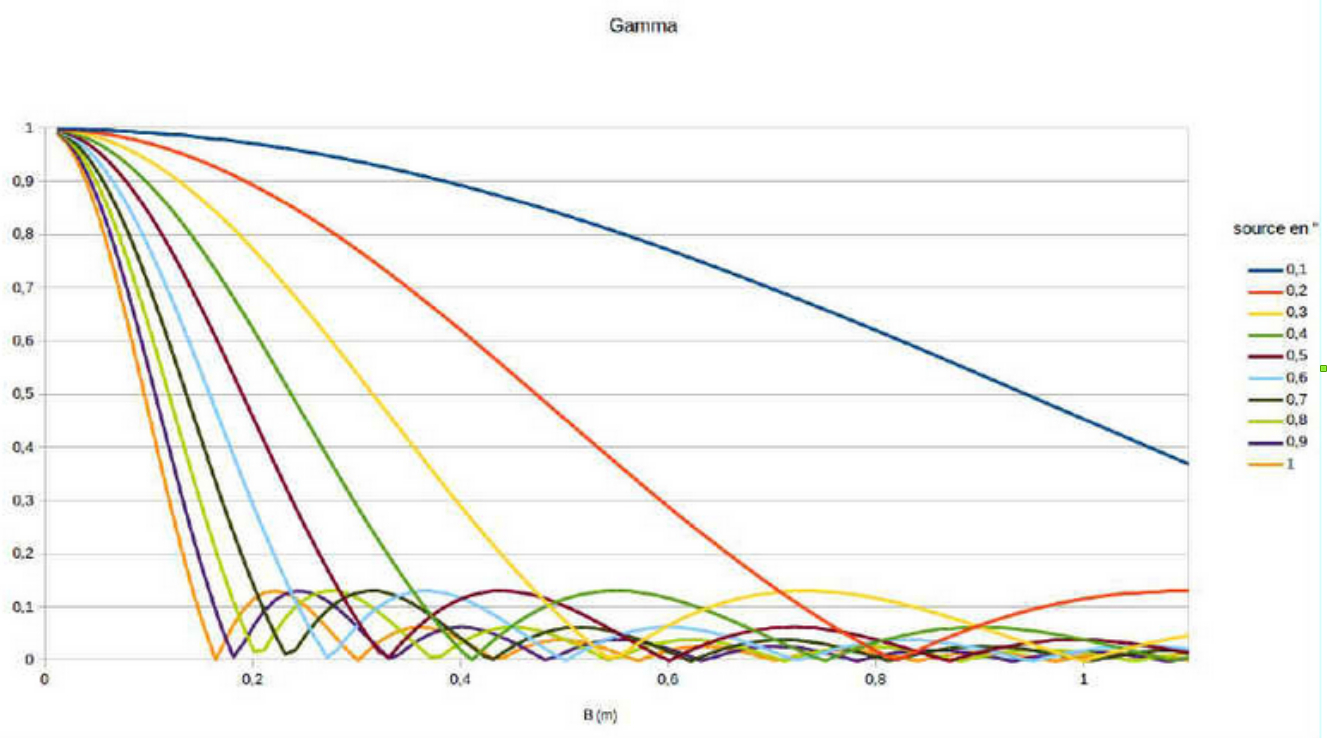
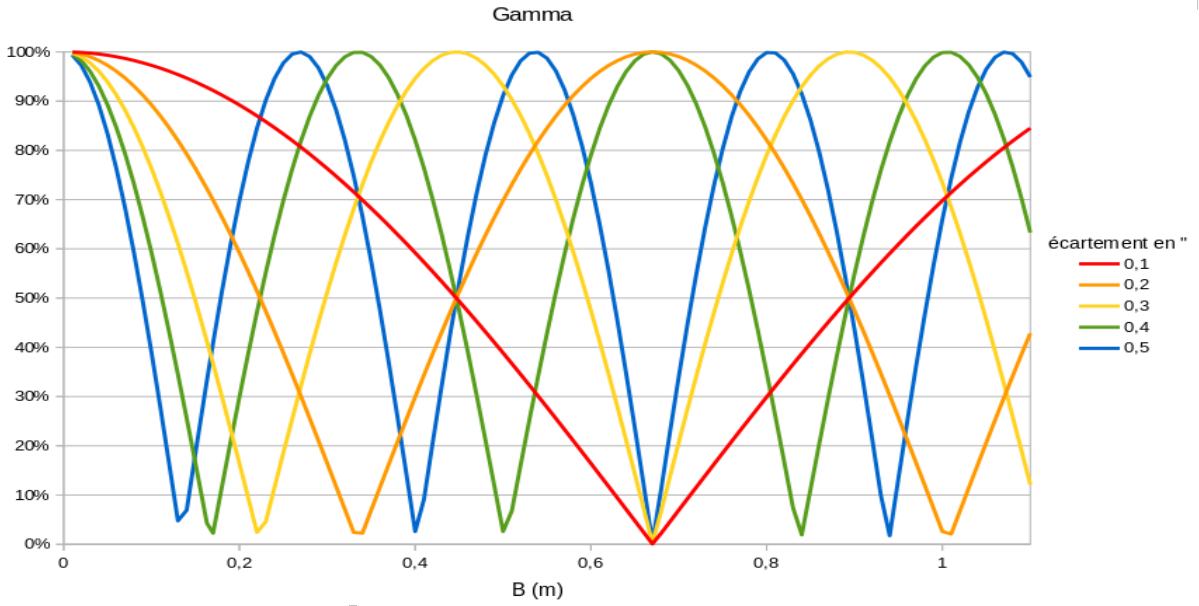
L’expression mathématique du contraste des franges d’interférence pour un disque uniforme (Figure 6) est une fonction de Bessel d’ordre 1 (J1(x)) dont le point d’annulation (Gamma = 0) intervient lorsque la dimension angulaire Alpha de la source est égale à la longueur d’onde de la lumière incidente, divisée par la base séparant les deux ouvertures. On peut donc, en recherchant la base B pour laquelle les franges disparaissent, obtenir la mesure du diamètre de cette source. De la même manière, pour une étoile double, en supposant que l’orientation des ouverture de l’interféromètre corresponde à l’orientation du couple d’étoiles, la séparation du couple peut être mesurée avec la disparition des franges d’interférences.
Mise en œuvre expérimentale
La difficulté de réalisation d’un dispositif optique permettant d’assurer une telle précision sur les chemins optiques a longtemps été un obstacle considéré comme incontournable dans le monde amateur. Malgré cela, les avancées technologiques issues notamment des travaux récents des pionniers de l’interférométrie optiques professionnelle, Antoine Labeyrie en tête, m’ont convaincu que les moyens simples de réalisation amateurs (tour et fraiseuse) sont à la hauteur d’un tel défi. L’objectif à donc été de réaliser dans un premier temps une poutre de Michelson de dimension réduite (106cm), placée devant un télescope Celestron 8 (203mm de diamètre) permettant l’obtention des franges d’interférence sur étoile, comme Michelson l’avait fait avec sa poutre de 6m devant le télescope de 2,5m du Mont Wilson. La première étape a été de réaliser à l’aide de 4 miroirs elliptiques de 50mm de petit axe, utilisés sur des télescopes de taille moyenne comme miroirs secondaires, une poutre à double périscope (Figure 9). Ces miroirs sont montés sur quatre supports réglables constitués chacun de deux plaques d’aluminium disposant de deux vis à pas micrométriques approvisionnés dans le commerce dans une configuration trou-traits-plan avec une bille acier de diamètre fixe. Cette configuration permet un réglage fin de l’incidence de chaque miroir avec seulement deux vis de réglages (au lieu de trois pour un système de collimation de miroir secondaire). La base mécanique de la poutre est un assemblage de règles de maçonnerie en aluminium servant à lisser des dalles de ciment, ainsi que des cornières en aluminium. Les miroirs externes sont montés sur des chariots navigant sur des glissières permettant de varier la valeur de la base de 30cm à 106cm. Par commodité, nous utiliseront la dénomination de M1, M2, M3 et M4 pour nommer les miroirs, avec M1 et M4 les miroirs externes, et M2 M3 les miroirs interne de la poutre (Figure 8).
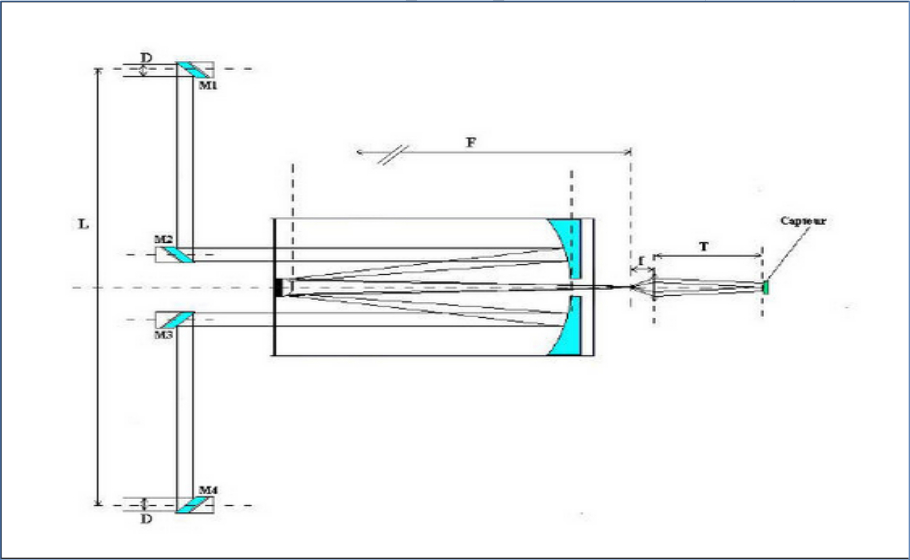
Le miroir M4, en plus du système de positionnement à glissière, est monté sur une platine de déplacement micrométrique linéaire, afin de régler la distance M1/M4 avec une précision de l’ordre de 5/10ème de mm. Il est donc possible, de régler la distance M1/M2 avec une simple réglet au millimètre et ajuster la distance M3/M4 avec la vis micrométrique du chariot dans une plage de 15mm. Nous voyons que cette précision n’est pas forcément suffisante au départ pour assurer la superposition des faisceaux incidents au niveau du foyer du télescope. Mais nous verrons plus loin que l’ajustement à la fraction de microns peut être obtenue avec un dispositif original constituant le cœur de l’interféromètre. L’ensemble est monté sur un cerclage en bois s’ajustant sur l’avant du télescope, à la manière d’un capuchon mais dont le poids (environ 5kg) constitue une contrainte pour la monture. Il a été nécessaire d’ajouter un ensemble de contrepoids très en arrière de l’oculaire (Figure 9), pour assurer l’équilibrage de l’ensemble.

Le premier essai d’obtention de franges à été effectué à l’aide d’un pointeur laser rouge, situé à 30m +/-0,1m du télescope. La caméra utilisée était une Basler ACE 640-100gm placée derrière une lentille de Barlow Celestron Ultima 2x, permettant d’obtenir une focale résultante de 4m. L’image présentée sur la Figure 10 , extraite d’une vidéo de 30s avec un temps d’exposition de 10ms, à été faite avec une base de 39cm. Les franges apparaissent sans aucune ambiguïté dans les speckles (défaut) du laser. Fort du constat de la présence des ces franges, nous avons réalisé une étoile artificielle afin de vérifier la validité du montage dans une perspective de mesure angulaire de dimension de source simple ou double.

La première mesure de diamètre angulaire
L’étoile artificielle est un trou calibré de 10 micromètres taillé au laser dans une plaque d’aluminium anodisée et vendue pour quelques dizaines d’euros par la société Thorlabs (Figure 11). Ce trou calibré est éclairé par l’arrière avec le laser (λ = 0,63 μm) ayant servi à l’obtention de la série de franges d’interférence précédente. Pour effectuer la mesure, le trou est placé a une distance de 9.9m +/-0,1m de l’interféromètre, afin de sous tendre une taille de source de 0,208’’ de degrés d’angle. Ce trou calibré est considéré avec une approximation raisonnable, comme un disque uniformément éclairé. La mesure des contrastes à différentes bases a été réalisée pour 16cm, 39cm, 67cm, 83cm et 106cm. (voir figure 12). Les conditions de prises de vues sont identiques à celles décrites précédemment (caméra, et séquences vidéos de prise de vue)

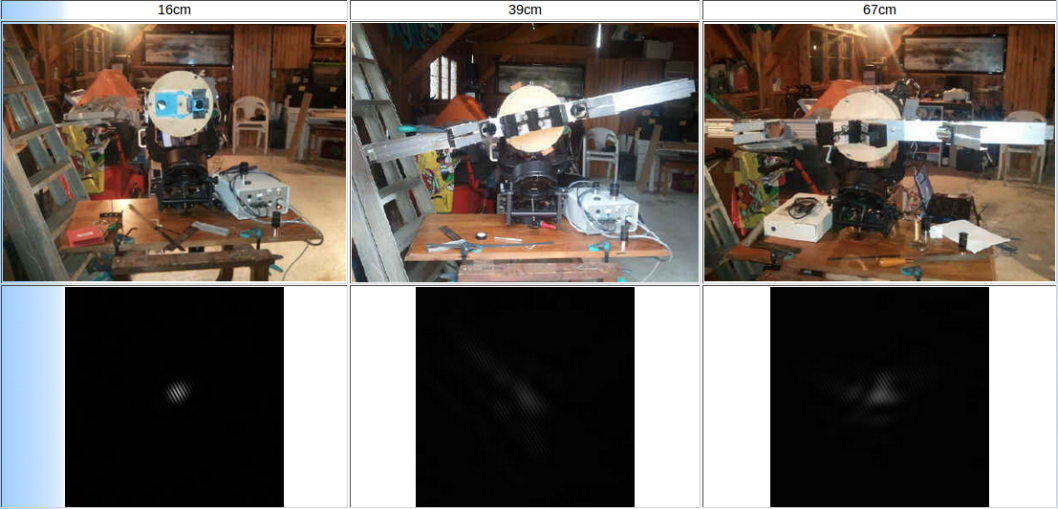
Lors de travaux amateurs que j’ai mené dans les années 2005/2009 sur les contrastes mesurés avec écran de Fizeau, j’ai mis au point une procédure d’extraction automatique du contraste des franges d’interférence à l’aide du Logiciel Iris de Christian Buil et basée sur l’extraction directe des intensités minimum et maximum, mais aussi en parallèle sur l’utilisation des transformée de Fourier lorsque le rapport signal/bruit des franges devient faible. Cette procédure fait état sur des franges simulées d’une précision d’extraction des contrastes de l’ordre de +/-4 %, ce qui représente une incertitude assez basse pour rendre les mesures expérimentales fiables. Le résultat des contrastes mesurés est visible sur la Figure 13.
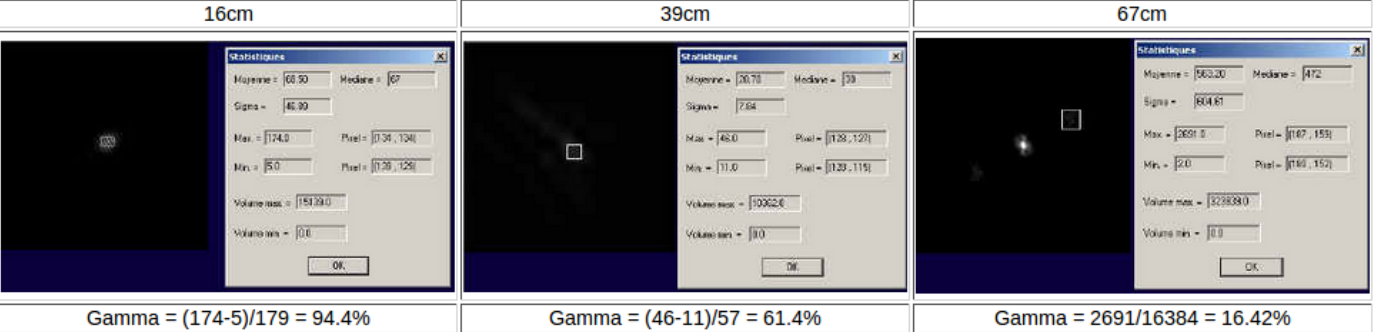
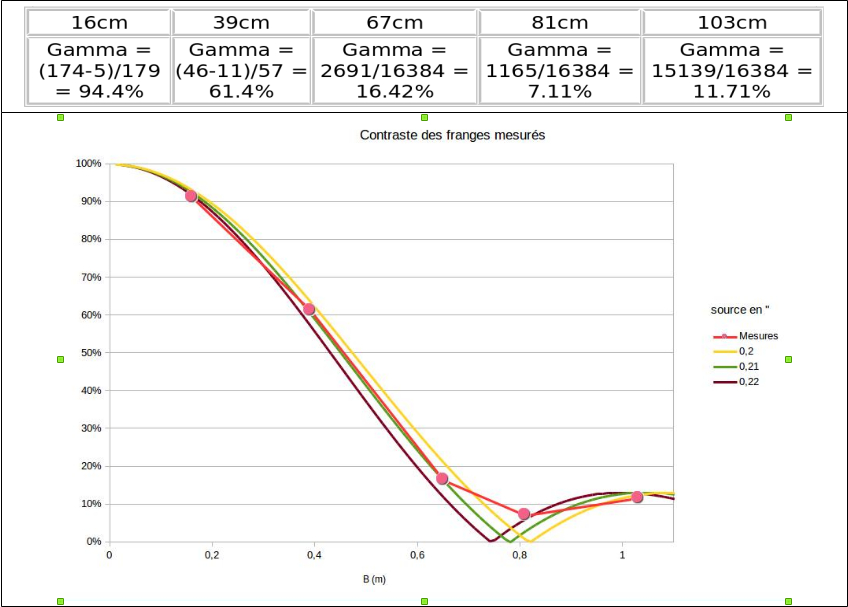
Les valeurs mesurées ont ensuite été insérées dans le tableau de valeur théoriques correspondant, et l’ajustement des courbes théoriques au nuage de point montrent une valeur optimale de l’angle sous tendu par la source de 0,21’’ d’arc. Cette valeur est a comparer aux 0,208’’ d’arc que l’on peut déduire de la connaissance de la taille de la source. Nous sommes donc à même de constater que cela fonctionne particulièrement bien, et que cette première mesure « de laboratoire » est très prometteuse. Il faut toutefois pondérer un quelconque enthousiasme d’une remarque liée à la physique du phénomène : cette mesure à été réalisée en condition mono-chromatique. Or une étoile est une source à spectre étendu. Cela veut dire que sous la condition d’une frange centrale centrée sur l’axe optique, autrement dit au milieu de l’image, le nombre de franges apparentes de part et d’autres peut être très grand. Mais si l’on additionne à ce premier réseau de franges, centré sur la longueur d’onde l1 un second réseau de franges, lui aussi centré sur sur l’axe, mais d’une longueur d’onde l2 différente de l1, la somme des intensités dans le plan image rendra les franges de moins en moins nettes lorsque l’on s’éloignera de l’axe.
La génèse de l’oculaire Frangeur
Dans le cas d’une étoile, dont la lumière est constitué d’une somme de longueur d’ondes différentes (le spectre de l’étoile), la somme des intensités de chacune des longueurs d’onde contribue à réduire le nombre de franges visibles (voir Figure 15). On définit ainsi une longueur, aussi appelée longueur de cohérence Lc, correspondant à la dimension de l’enveloppe des franges au sein de laquelle les franges restent discernables. Cette longueur Lc est donnée par la relation suivante extraite de la littérature (c’est en particulier le dernier terme de cette égalité qui nous intéresse en premier lieu) :
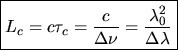
avec lambda0 la longueur d’onde centrale d’observation de la source, et Dlambda la largeur spectrale de cette source.
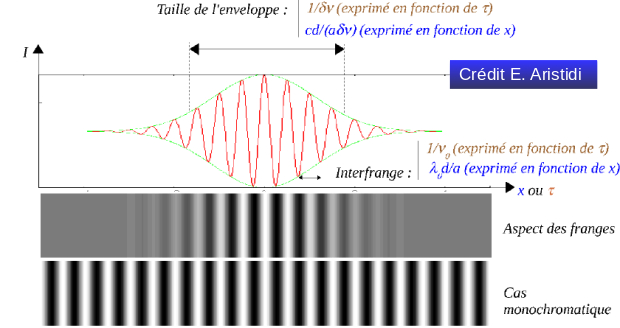
Il apparaît immédiatement que plus la source comporte de longueurs d’ondes différentes (grande largeur spectrale), moins les franges seront nombreuses, car brouillées, de part et d’autres de la frange centrale. Le tableau de la Figure 16 nous montre les longueurs de cohérences associées à différentes sources lumineuses, de largeurs spectrales différentes. On constate que dans le cas d’un laser Hélium Néon (ou son équivalent en diodes laser), la largeur spectrale est tellement fine que la longueur de cohérence avoisine les 30 centimètres. Autrement dit, dans le cas de l’essai précédent, le très grand nombre de franges visibles de part et d’autres de la frange centrale ne posait aucun problème sur les longueurs de trajets parcouru par la lumière sur chaque chemin optique.
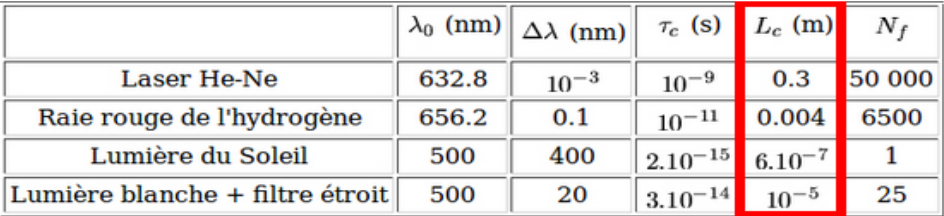
Il n’en est pas de même dans le cas de la lumière du Soleil par exemple, où la longueur de cohérence chute à 0.6µm,et le nombre de franges visibles est de 1… L’une des solutions pour améliorer la visibilité de ces franges est donc de filtrer la lumière de l’étoile, pour augmenter la longueur de cohérence, et ainsi augmenter le nombre de franges de part et d’autres de la frange centrale. Ainsi on peut en lumière blanche obtenir une longueur de cohérence d’environ 10µm, donc quelques dizaines de franges, avec un filtre de 20nm de bande passante. Cette solution semble séduisante pour obtenir des franges, mais elle comporte un problème, plus le filtre est étroit, moins l’on collecte de lumière dans le plan focal. Il s’agit donc de trouver le compromis entre la magnitude limite de l’objet accessible par l’interféromètre, conditionnée par les dimensions des miroirs M1 et M4, et le nombre de franges que l’on pourrait obtenir avec une longueur de cohérence donnée par la largeur spectrale de la source.
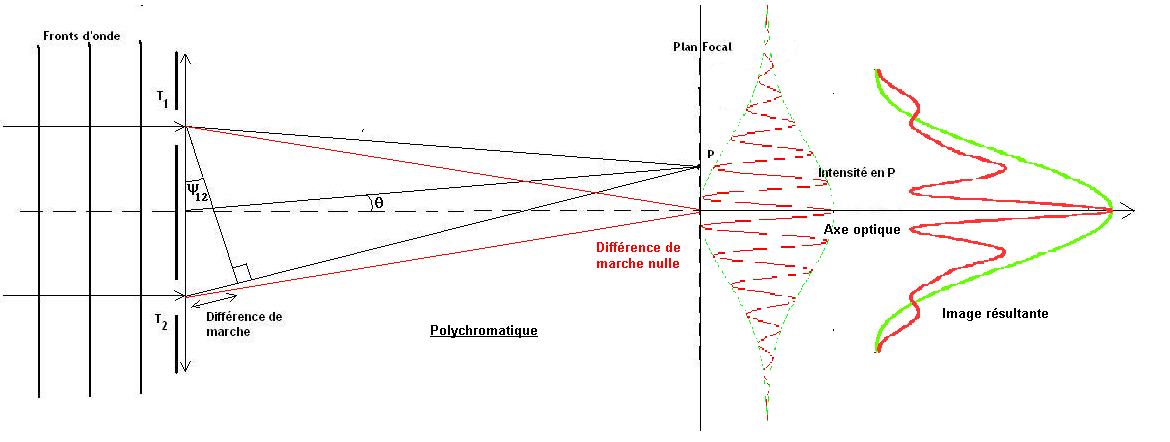
Pour bien comprendre la difficulté de l’expérience de la poutre de Michelson, liée à une grande largeur spectrale de la source, la figure 17 nous montre le cas idéal de l’expérience du masque de Fizeau. Pour un masque posé devant le tube du télescope, si l’étoile est centrée sur l’axe de ce dernier, le front d’onde issu de l’étoile arrive simultanément sur le trou T1 et sur le trou T2 . Les rayons passant alors par chaque ouverture vont parcourir un trajet identique et interférer sur l’axe optique, produisant la frange centrale. Cette frange centrale constitue donc la position ou se rejoignent les rayons optiques avec une différence de marche nulle. Lorsque l’on s’éloigne de la frange centrale, les franges latérales sont atténuées en proportion de la propriété de longueur de cohérence que nous avons vue précédemment. L’image résultante, visualisée sur la partie droite de la figure 17, sera constituée du réseau de franges atténué sur les bords et multiplié par la figure de diffraction lié à la taille des trous T1 et T2 . C’est exactement ce que nous avons pu constater sur la figure 2. Les choses se compliquent dans le cas de la poutre de Michelson. Le principe est détaillé sur le schéma de la figure 18. En effet, les rayons lumineux arrivant sur le télescope, ayant parcouru des trajets M1/M2 et M3/M4 arriveront à l’entrée du télescope avec une différence de marche inconnue car dépendante de l’erreur sur les longueurs de chemins liées à la construction de la poutre. L’effet immédiat est donc que le point ou se rencontrent ces rayons lumineux avec une différence de marche nulle (ce qui correspond à la frange centrale du réseau de franges d’interférence), ne se trouve plus nécessairement sur l’axe optique. Le réseau de franges sera décalé par rapport à l’axe et l’image résultante correspondra alors à la figure de diffraction liées aux trous d’entrée du télescope (ligne verte) avec peu de franges voire pas du tout. Dans l’exemple de la figure 18, la position du point du plan focal, où la différence de marche est nulle (donc correspondant à la frange centrale du réseau de franges), se trouve décalé au dessus de l’axe. On voit immédiatement que si la différence de marche est supérieure à la longueur de cohérence, il n’y aura pas de franges dans la figure de diffraction sur l’image résultante. La question que l’on peut alors se poser est : existe-t-il un moyen optique de ramener la frange centrale sur l’axe optique en compensant la différence de marche de l’un ou l’autre des rayons lumineux ?
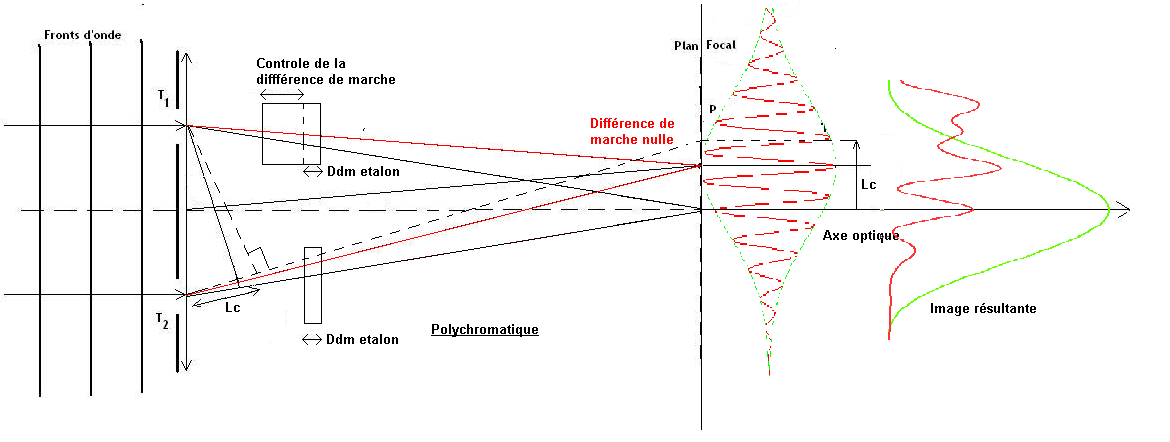
La solution, imaginée par Antoine Labeyrie, consiste à insérer le long de chaque trajet optique un milieu transparent, l’un d’épaisseur fixe et servant de différence de marche étalon (ddm), l’autre d’épaisseur variable. En effet, le trajet optique, dans sa définition technique, est égal au produit de l’indice optique du milieu traversé multiplié par l’épaisseur de ce milieu. Donc si l’on utilise une cale d’épaisseur fixe, pour le trajet du trou T2 (Figure 18) et une épaisseur d’un matériau de même indice mais dont on peut faire varier l’épaisseur en deçà ou au-delà de celle de la cale optique, on est en mesure de contrôler finement la position du point de rencontre des rayons de différence de marche nulle dans le plan focal du télescope.
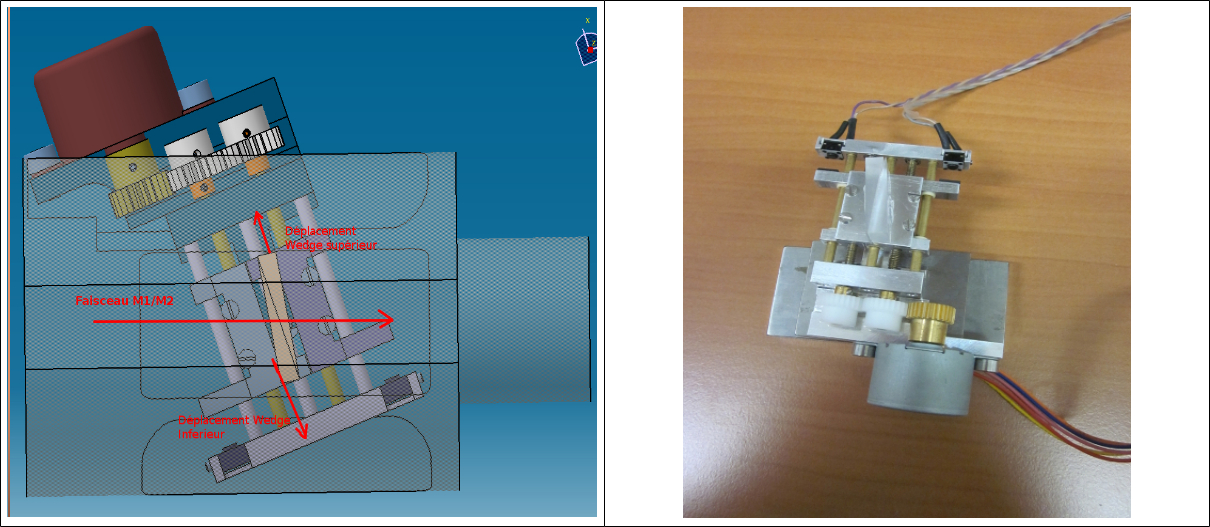
Pour réaliser cette ligne optique d’épaisseur variable, l’astuce technique consiste à utiliser deux prismes montés tête bêche, que l’on fait glisser le long de leurs hypoténuse. Ainsi un rayon traversant les deux prismes en arrivant perpendiculaire au grand coté du premier prisme, ressortira après avoir traversé une épaisseur de verre variable que l’on peut contrôler en bougeant symétriquement la position des deux prismes (figure 19). Cette véritable ligne à retard optique est insérée dans un oculaire et pilotée électroniquement afin d’assurer la compensation des trajets optiques sans provoquer de vibrations lors de la recherche du point de centrage des franges sur l’axe (figure 20)

L’angle des prismes défini la longueur optique que l’on est en mesure de balayer. L’oculaire frangeur que nous avons réalisé permet de balayer une différence de marche de 3mm (+/-1.5mm autour de l’épaisseur de la cale optique du trajet T2 ). Cela reviens donc à dire que si nous avons une précision de positionnement des miroirs M1 et M4 sur la poutre de Fizeau Michelson inférieure à 3mm, nous sommes en mesure de compenser cet écart de chemin optique et de retrouver les franges sur l’axe du télescope. Les deux fenêtres de la ligne à retard sont suivies par une combinaison de lentilles cylindriques croisées formant un oculaire de Galilée anamorphoseur. Cette partie de l’oculaire permet de dilater les franges le long de l’axe des trous (ou des poutres), et de les compresser verticalement, afin d’en améliorer la visibilité. Le premier test de cet oculaire frangeur à été mené avec succès, grâce à un masque de Fizeau, afin de vérifier la possibilité de modification de la position des franges. En effet, les réglage propres à l’oculaire frangeur sont de 2 types. Nous l’avons vu, la pupille de gauche sur la figure 20 permet de régler l’épaisseur optique nécessaire à l’égalisation des chemins, en deçà de la longueur de cohérence. La fenêtre de droite à pour rôle d’accueillir le faisceau entrant par le chemin du trou T2 dans le cas du masque de Fizeau, ou encore le faisceau issu du chemin M3/M4 de la poutre Fizeau Michelson. Or dans le cas de ce dernier appareil, l’incertitude de longueur de chemin n’est pas le seul obstacle, il en reste un second, qui est l’incertitude sur l’inclinaison du rayon à l’entrée du télescope collecteur. Autrement dit, par construction, il est possible que l’image transmise au travers de cette fenêtre soit décalée vers le haut, ou vers le bas. Il a donc fallu trouver un moyen simple de compenser cet écart angulaire en réalisant cette cale optique dans un matériau souple, emprisonné entre deux lames de microscope, et dont on fait varier l’inclinaison en pressant sur l’une des lames. Ce matériau souple et transparent, constitué d’un gel silicone que l’on peut approvisionner dans les magasins de bricolage, permet donc de fabriquer un prisme d’angle réglable, qui facilite l’alignement des images respectives des deux chemins optiques considérés.

Premiers résultats
Après validation du fonctionnement de l’oculaire Frangeur c’est seulement à l’automne 2018 que j’ai put effectuer le montage complet de l’interféromètre Poutre et Oculaire frangeur (figure 21). A noter immédiatement que le bras de gauche de la poutre, dispose d’un chariot à déplacement micrométrique, permettant à la fois un déplacement fin du miroir M4 et de balayer finement (avec une précision de l’ordre de quelques centièmes de mm), la zone au sein de laquelle j’espérais obtenir les franges d’interférences. A noter que le déplacement propre de ce chariot se fait dans une plage de +/-7,5mm autour de sa position médiane. L’idée pour obtenir le co-phasage des deux chemin est donc la suivante : Caler au mieux les longueurs des deux chemins optique, avec une incertitude de l’ordre du millimètre, puis balayer à l’oculaire frangeur la zone de différence de marche (3mm), jusqu’à voir apparaître les franges lorsque la ddm deviens inférieure à la longueur de cohérence de la source. L’un des premiers écueils de l’instrument est le temps de réglage de la collimation des deux faisceaux. Il faut bien se rendre compte que là ou l’habitude d’un télescope standard oblige à travailler sur 3 vis de réglages (enfin dans le cas d’un réfracteur Schmidt-Cassegrain), la poutre de Fizeau Michelson implique 8 vis de réglages supplémentaires soit 11 vis au total pour aligner les images issues des deux poutres. Après deux séances d’apprentissage, le temps de collimation est de l’ordre d’une vingtaine de minutes. Ici les premiers essais de collimation ont été réalisé sur l’étoile Procyon, au foyer du C8, caméra ASI224 pose de 10ms. C’est seulement après avoir fait cette collimation au foyer (figure 22 image de gauche) que l’ajout de l’oculaire frangeur permet d’affiner au mieux la superposition des deux spots. Le réglage de la cale optique permet de ramener le spot issu de M1/M2 et le spot de M3/M4 à la même hauteur, le long de l’axe des deux poutres. La superposition horizontale des deux spots se fait alors en jouant sur la mise au point du télescope. C’est cette dernière qui amène les deux spots à se superposer le long de l’axe des poutres (figure 22 image de droite, Bételgeuse caméra ASI224 temps de pose 30ms ).

Comme dit précédemment, l’oculaire frangeur est doté d’un système anamorphoseur permettant d’allonger les spots le long de l’axe horizontal (ou plus précisément le long de l’axe des poutres) et de compresser ces spots le long de l’axe vertical. Cela permet d’améliorer sensiblement la lisibilité des franges qui sans cela, apparaîtraient en limite de sous échantillonnage le long de l’axe horizontal. Pour le premier essai d’obtention des franges, l’écartement M1/M4 est réglé arbitrairement à 662mm. Un premier balayage de la différence de marche (ddm) de 3mm à l’aide de l’oculaire frangeur n’a pas permis de trouver les franges tant attendues. Le chariot du M4 est alors déplacé par pas de 1,5mm dans un sens à l’aide de sa vis micrométrique, et l’on recommence l’opération de balayage de ddm jusqu’à obtenir un résultat. Les caractéristiques mécaniques du système de balayage de la ddm permet de parcourir ces 3mm en à peu près 2 minutes.

C’est lors de la troisième tentative que les franges sont obtenues à 657mm d’écartement. Les 7 à 8 franges obtenues sur Bételgeuse (Figure 23) sont particulièrement marquées, et présentes tout au long de la vidéo de 30 secondes acquise avec une caméra ZWO ASI224 à 30ms secondes de pose, gain numérique à 400. Le temps de pose est un peu long, ce qui peut expliquer l’aspect un peu empâté des franges, il s’agit d’un effet connu de translation par effet de tip/tilt, seule composante de la turbulence affectant la visibilité de ces franges. Ces dernières apparaissent inclinées. Ce phénomène s’explique par le défaut d’inclinaison des bras de la poutre avec les fenêtres de l’oculaire frangeur. Ce défaut a été corrigé lors du deuxième essais sur Sirius. On peut noter aussi que par construction, ce premier prototype de poutre de Fizeau Michelson sur monture équatoriale à fourche ne peut fonctionner qu’au voisinage du méridien. En effet, les contraintes de poids sur l’un et l’autre bras sont différentes si l’on s’éloigne du méridien. Cela se traduit rapidement par une déformation de l’un ou l’autre des spots et donc une modification de la structure des franges que nous avons observé quelques dizaines de minutes après le passage de Bételgeuse au méridien. Pour l’occasion, on pourra noter que Bételgeuse au moment de l’obtention des franges les plus marquées, était à 49°29’ de hauteur.

Sur la même base en écartement, le test suivant a été réalisé sur l’étoile Sirius. Les conditions de prises de vues étaient plus délicates, car la culmination de l’étoile au méridien s’est faite pour une hauteur sur l’horizon de « seulement » 26°16’. On pourra remarquer d’ailleurs l’effet de la réfraction atmosphérique sur la troisième image de la figure 23 avec une coloration bleutée au dessus des franges et plutôt portée sur le rouge en dessous. Conditions de prise de vue ZWO ASI 224 pose de 9ms gain à 425 séquences de 30 secondes. Dans les deux cas, pour Bételgeuse et Sirius, les images présentées sont les meilleurs extraits de franges issues de séquences vidéo de 30 secondes.
Conclusion
En conclusion, nous avons fait la démonstration que le domaine de l’interférométrie optique, est accessible avec des moyens amateurs. Cet article représente un premier pas vers la réalisation d’appareils interférométrique optique de dimension modeste dans un premier temps, mais que l’on pourra vraisemblablement étendre en terme de longueur de base et de cibles potentielles pour faire des mesures, voire de la reconstructions d’images. En effet, nous avons pût établir qu’il est possible de résoudre une source simple ayant des dimensions angulaires inférieures au pouvoir de résolution du télescope utilisé pour l’expérience présentée ici. Le deuxième point démontré ici est qu’il est possible de travailler sur des sources étendues spectralement, ce qui constitue la difficulté principale pour assurer la réalisations d’instruments interférométriques dans le domaine optique, ou la longueur de cohérence n’est que de quelques microns. Il est remarquable d’obtenir des informations de taille angulaire accessibles uniquement avec un télescope de 1 mètre de diamètre à l’aide d’un télescope de « seulement » 20cm et nous avons fait la démonstration que cela était possible grâce à un appareil de type « oculaire frangeur ». Les techniques de mise en œuvre sont maintenant connues et leur mise à l’épreuve dans le domaine observationnel reste encore à faire, pour le domaine des étoiles doubles, et pourquoi pas, aussi, sur des cibles uniques accessibles à des interféromètres de l’ordre de quelques mètres. Toutefois, l’étape présentée ici montre qu’il est déjà possible, avec des moyens modestes, d’aborder et d’envisager l’interférométrie optique en astronomie amateur.