Sommaire

Introduction :
Pour faire suite à la première page de ce site consacrée à l’interférométrie des tavelures (certains paragraphes ici seront redondant avec la partie I), le but de cette seconde page est de montrer la mise en œuvre de l’expérience, et l’extraction des données de position et d’angle sur un télescope. L’expérience présentée ici est le résultat de 2 nuits d’observations faites dans le cadre de l’association T60 (association du télescope de 60cm de l’observatoire du pic du midi ) au cours d’une mission ayant eu lieu du 30 juin au 6 juillet 2008. Afin de saisir le détail du traitement, il est recommandé de lire la description de la méthode d’analyse des séquences vidéo de tavelures, détaillées sur les pages de A. et S. Rondi, pages dont le lien est présenté sur la partie Bibliographie de ce compte rendu.
L’interférométrie des tavelures est une idée relativement ancienne, issue principalement des travaux de A. Labeyrie (1970), et quelques pionnier, qui après avoir effectué des tentatives fructueuses en interférométrie de Fizeau-Michelson (que l’on pourrait qualifier d’interférométrie « classique »), se sont penchés sur la structure des images en pleine ouverture, et y ont constaté ce que Paul Couteau cite dans son ouvrage de référence sur le mesure des étoiles doubles « L’observation des étoiles doubles visuelles »: A. Labeyrie et ses collaborateurs (1970) atteignent le fond du problème en exploitant l’ensemble de l’image à pleine ouverture. Ils étudient d’abord la formation de l’image d’une étoile, perturbée par l’atmosphère, au foyer d’un grand télescope. La cinématographie permet une étude détaillée de la structure complexe de cette image, qui se présente sous la forme d’une grappe de raisins, dont chaque grain est animé d’une vive agitation et est d’une durée de vie très courte. Ils partent de l’idée que cette image résulte d’effets d’interférences entre le faisceau incident et les fluctuations spatiales aléatoires de phases. Un grain n’est autre que la transformée de Fourier de la pupille du télescope, c’est l’image de diffraction de l’étoile. Dans le cas d’une binaire, chaque grain contient l’information, l’ensemble de la grappe est double, mais le décalage est très petit, plus petit que la dimension de la figure de diffraction. » La technique simple sur le principe, n’est pourtant pas évidente à mettre en œuvre. En effet, la principale difficulté réside dans le fait de pouvoir figer ces « grappes » dues à la turbulence de manière quasi instantanée. Les temps d’exposition nécessaire à l’obtention de ces « tavelures » sont de l’ordre de quelques dizaines de millisecondes, voire moins. Inutile de préciser que dans ces conditions, il faut faire entrer en conjonction plusieurs éléments techniques afin d’obtenir des clichés exploitables sur une étoile, dont le flux lumineux, par une calcul simple, se résume à quelques dizaines de nano watts pour une étoile de magnitude 0 dans un télescope de diamètre amateur standard. Les difficultés sont les suivantes : Dans un premier temps, avoir un télescope collectant beaucoup de lumière, donc un diamètre important. Le T60 est alors en soi l’un des candidats le plus sérieux à la mise en place de ce genre d’expérience dans le monde de l’astronomie amateur. La deuxième difficulté est d’avoir un échantillonnage suffisant pour obtenir ces « grains » de lumière en détails. Typiquement, le diamètre de la tache de diffraction théorique pour un télescope de 60cm est (en fonction de la longueur d’onde à laquelle nous allons travailler), de 0.2’’ d’arc. Nous devons donc, d’après ce que nous enseigne le théorème de Shannon, avoir un échantillonnage d’au moins 0.1’’ d’arc. Il faut donc travailler avec une focale très importante (supérieure à 20m dans le cas du T60). La troisième difficulté réside dans le système d’acquisition. L’obtention des tavelures nécessite des temps d’exposition tellement courts, que les systèmes d’imagerie numériques utilisés par les professionnels sont pour la plupart des caméras rapides intensifiées, hors de portés de nos budgets amateurs. Or depuis quelques années, les caméras à faibles coûts que l’on peut trouver sur le marché ont des performances en terme de sensibilité, comparables à certaines caméras professionnelles. C’est notamment le cas à l’heure actuelle des caméras de type WATEC 902H2 Ultimate, affichant une sensibilité de 0.0001 lux, sur une matrice de 768×494 pour un prix de quelques centaines d’euros. Dans l’esprit de la voie explorée par A. Rondi et S. Rondi dans le domaine amateur sur l’Observation d’étoiles doubles par interférométrie des tavelures en 2005 (http://www.astrosurf.com/rondi/t60/crabe-tambour/speckle.htm), nous souhaitions faire quelques tests en utilisant cette caméra associée à un système de grandissement simple (tirage oculaire) permettant de travailler à une focale peu courante pour le T60 (>20m). L’expérience acquise dans le domaine de l’interférométrie classique à diaphragme de Fizeau, associée aux puissantes méthodes de traitement numérique de l’image, rendent possible une véritable « restauration » du pouvoir théorique du télescope, pouvoir théorique qui, nous le savons bien, est limité par la turbulence atmosphérique, et plus particulièrement par la dimension de la zone de cohérence du front d’onde aussi connue sous le nom zone de Fried. Les caractéristiques dimensionnelles de la tache de Fried au Pic sont très bien connues par les professionnels. A ce titre, je ne peux que reprendre un extrait d’un e-mail de Jean Lecacheux posté sur la liste Aude le 03 Oct 2006 lors de la résolution d’une étoile double (étoile du catalogue Couteau) qui fut nécessaire pour appréhender l’occultation de cette étoile par l’astéroïde Vibilia en 2006 : >>Ensuite on attend de bonnes conditions, lesquelles au Pic arrivent deux ou trois fois par semaine, sauf accident météo…Je n’ai tenté cette observation que le lendemain de l’occultation, réussissant du reste du premier coup. Les étoiles étant dans ce cas de magnitude 10, il fallait une pose de quelques dixièmes de seconde (j’ai choisi 0.3 seconde).Il était donc impensable de figer réellement les tavelures. Tous mes clichés montrent des tavelures plus ou moins déformées et floues, c’est-à-dire plus ou moins bougées. Je sélectionne évidemment les moins bougées et les moins floues parmi des centaines et des centaines….Quand l’image est mauvaise (disons quand le seeing fait 2″), les régions de Fried mesurent seulement 5 centimètres et sont minoritaires. L’image focale renferme de nombreuses tavelures très peu contrastées en mouvement très rapide sur un fond diffus. Quand l’image devient bonne, les régions de Fried deviennent décimétriques, les tavelures sont peu nombreuses, plus contrastées et plus lentes. Quand le seeing descend à 0″.5 en moyenne, certains instants fugitifs atteignent alors un seeing record de peut-être 0″.3 ou 0″.25. Les régions de Fried devenues grandes, parfois de 50 cm, se connectent entre elles, occupent maintenant une place majoritaire sur le miroir, et on ne voit plus qu’une tavelure principale contenant la majorité de l’énergie lumineuse, peut-être flanquée d’une ou deux tavelures satellites pâles, placées sur ce qui dans un cas d’école s’appellerait « anneau d’Airy »… La nuit de l’observation j’ai considéré que 2.5 % des imagettes enregistrées (de 32×36 pixels, soit 3 ».5 x4″) méritaient d’être sélectionnées. Au total 61 imagettes. Pour le Pic, c’était là une bonne qualité habituelle. Dans les nuits de qualité plus extrême que nous appelons « le Grand Pic », qui se présentent en moyenne une fois ou moins d’une une fois par mission de 10 jours -mais parfois 2 ou 3 nuits de suite !- j’aurais peut-être gardé 25 % ou 50 % des imagettes. Fort de l’ensemble de ces informations, nous avons donc consacré 2 nuits à mettre en œuvre cette technique d’observation, en voici les résultats :
Nuit du 30/06 au 01/07/2008 :
-Mise en place du système d’acquisition. Nous avons dans un premier temps essayé d’obtenir une image uniquement basée sur les éléments que nous avions montés là haut (bague allonge Meade, bague monture C pour la Watec 902H2, et bague adaptation sur PO de 2 pouces, mais le tirage était insuffisant pour obtenir une bonne mise au point. Fort heureusement, en regardant de manière plus précise dans le jeu de bagues propres au T60, nous avons trouvé ce qu’il fallait pour permettre le montage.
Le système d’acquisition se compose d’un ensemble de bagues, oculaire et Barlow classiques dans un montage par tirage oculaire :

De la gauche vers la droite, nous avons la bague allonge du PO du T60 ; suivie de la bague support du correcteur de champs, destinée à l’Audine, puis une bague « custom », tournée pour l’occasion, permettant d’insérer un oculaire monté sur une Barlow Celestron x2. Le diamètre extérieur de cette bague est de 50mm, ce qui la destinait au départ à être montée directement dans le porte oculaire. Malheureusement, le tirage insuffisant pour faire la mise au point a nécessité de trouver une astuce. Par bonheur, cette bague dispose (sur sa partie inférieure), d’un filetage intérieur compatible avec la bague de fixation de l’Audine. Nous avons donc pu visser l’ensemble constitué des 3 bagues de droite sur la bague Audine, qui s’insère elle-même dans la bague allonge de gauche. Nous pouvons voir sur les images suivantes l’ensemble monté sur le porte oculaire.
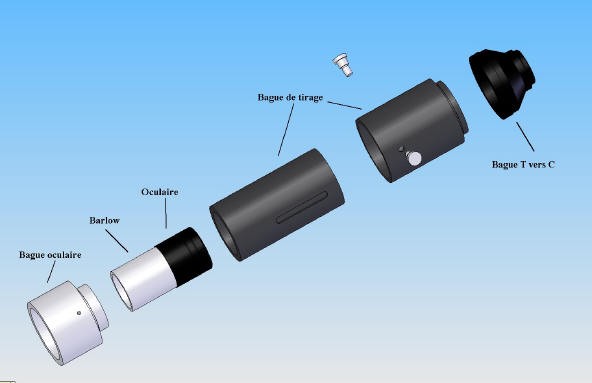

L’ensemble constitue un montage d’environ 40cm de long, mais le poids étant raisonnable, il n’y a apparemment pas de contrainte énorme sur le Porte oculaire. Connaissant le tirage de la bague Meade et la distance Oculaire capteur, nous pouvons calculer l’échantillonnage théorique du système : (La focale objectif tient compte de la présence de la Barlow, le T60 ayant une focale de 2135 +/-5mm)

La caméra est suivie d’un numériseur Pinnacle Dazzle video recorder, du même type que celui utilisé pour la manip d’occultation d’étoiles. Les vidéos acquises sont des AVI enregistrés sous Virtualdub en mode Raw. La cadence est de 25 ips, le temps de pose annoncé par le datasheet de la caméra est de 20ms. Le premier constat est que le pointage n’est pas évident. En effet, à ce niveau d’échantillonnage, le champ de la caméra est de 65×42’’ d’arc, ce qui est tout de même très peu. Le problème a été grandement simplifié par l’utilisation de la lunette guide que nous avons réalignée pour l’occasion, et de l’oculaire réticulé du T60, dont la particularité est d’avoir un double réticule. Constat amusant, le carré central de cet oculaire donne un champ proche de celui de la caméra. Le tour est donc joué. Le télescope pointant de manière correcte à quelques minutes, il suffit ensuite d’affiner en manuel le pointage avec la lunette guide, et l’on a l’étoile sur l’image. Le premier essai a été réalisé sur Vega (Mag 0.03)

Les speckles sont très marquées sur quasiment toutes les images de la vidéo (l’image présentée précédemment est en visu logarithmique). Nous avons acquis plusieurs vidéos de 50 secondes environ (soit plus de 1200 images), cela représente donc un espace de stockage nécessaire très important (600 mégaoctets par vidéo). Donc si la manip vous tente, prévoir un très gros disque dur !!!!! Sur l’image suivante, nous pouvons voir une image extraite de la vidéo montrant de manière très nette les tavelures. A titre de comparaison, nous présentons l’addition de 600 images pour voir ce que donne une pose équivalente de 12 secondes. En comparaison, nous avons rajouté la simulation (à la même échelle) de l’image de diffraction obtenue à l’aide de l’excellent logiciel Aberrator (http://aberrator.astronomy.net/).

On voit parfaitement les dégâts causés par la turbulence !! En tout cas, ces vidéos sont rassurantes au sens ou les tavelures sont effectivement présentes, et parfaitement visibles. Pour aller plus loin dans la caractérisation du système d’acquisition, nous avons choisi de travailler au cours de cette première nuit sur 3 étoiles de magnitudes et de séparation différentes (voir plus loin). Les images suivantes, nous montrent, comme nous l’avons fait pour Véga, une image sélectionnée parmi celles correspondant à la meilleure visibilité des tavelures. On y trouve aussi la somme de 600 images (12 secondes de poses), et une simulation correspondant au couple étudié.
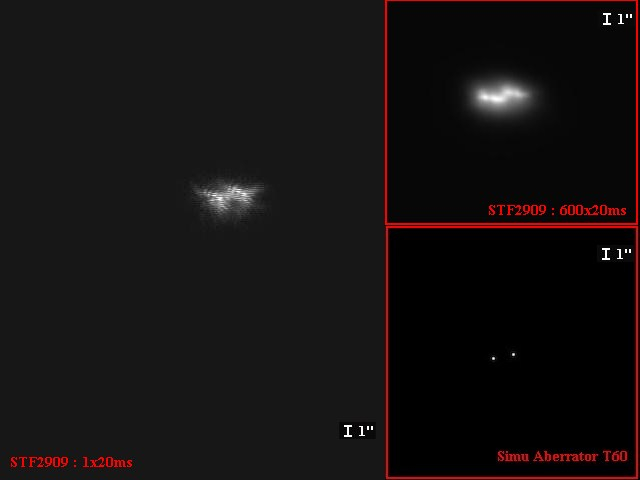


La nuit s’est donc achevée sur les premières acquisitions, et la journée du lendemain fût consacrée à chercher comment extraire de ces vidéos, l’information tant convoitée, à savoir la valeur de la séparation des composantes de ces couples d’étoiles. La vision des vidéos laissant tout de même entrevoir les couples noyées dans ces « grappes de lumière », la question se posait de savoir quelle était la meilleure méthode pour extraire l’info, mais aussi jusqu’à quelle séparation minimum nous sommes en mesure d’obtenir un résultat. Le paragraphe suivant revient brièvement sur les méthodes connues et déjà mises en oeuvre.
Discussion sur l’extraction de la séparation des couples
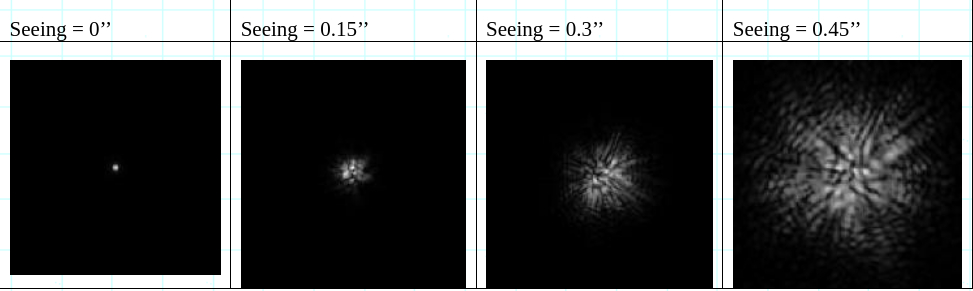
En utilisant quelques simulations sous le logiciel Abberator (en insérant une composante de turbulence atmosphérique), il est simple de se rendre compte de la problématique. Le tableau suivant montre, pour une étoile simple, les figures obtenues au T60 pour différentes valeurs de seeing :
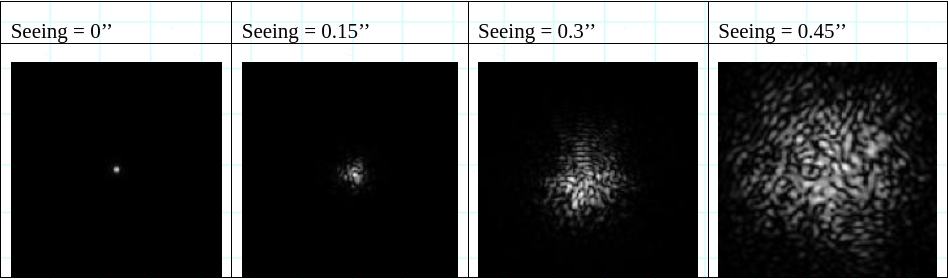
Chaque grain dans l’image est une reproduction déformée par la turbulence, de l’image de diffraction présentée à gauche. Pour se rapprocher de nos images expérimentales, nous devons aussi tenir compte d’un facteur que nous n’avions pas encore pris en compte, il s’agit de l’aspect chromatique. En effet, les tavelures que nous avons obtenues ne sont pas filtrées spectralement.Les tavelures originellement en couleurs, sont converties en monochrome par la caméra :
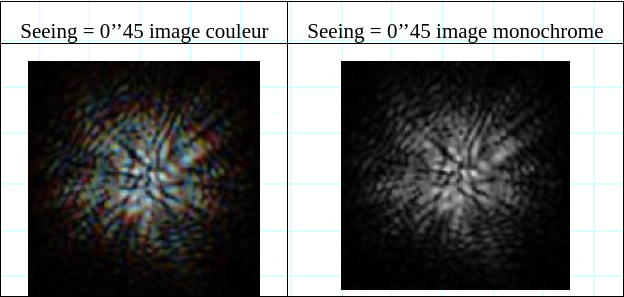
Les simulations donnent alors des images correspondant morphologiquement mieux à ce que nous montre les vidéos expérimentales :
Quelles sont alors les solutions mathématiques pour « restaurer » l’image de diffraction. Ces solutions dérivent d’analyses fréquentielles de l’image et sont connues sous le vocable d’auto corrélation et de cross corrélation. Ces méthodes ont été notamment discutées par A. et S. Rondi lors de leurs premières expériences sur le sujet de l’interférométrie des tavelures (voir références de leurs pages dans la partie bibliographique). Ces deux méthodes sont des méthodes de convolution de l’image soit par elle-même (auto corrélation), soit par son propre carré (cross corrélation). Ces 2 méthodes sont plus ou moins simplement applicables à l’aide d’un logiciel comme Iris de C. Buil. Une voie à explorer est peut-être celle de méthode de type « super-résolution », citée sur les pages de Patrick Lailly, mais je ne connais pour le moment pas le détail de ces algorithmes. Ces fonctions de corrélation sont facilement réalisables sous Iris en utilisant soit une fonction de type « Fcorrel » décrite dans l’aide de commande de Iris, soit en passant dans le domaine fréquentiel en utilisant les produits des transformées de Fourrier des images que l’on veut corréler. La séquence de commande de génération de l’auto corrélation dans le domaine spatial sous Iris peut s’écrire sous la forme : (l’exemple ci-dessous est appliqué à la vidéo de Véga dont le nom générique des images est Vega_foc_4)

Pour une intercorrélation (de l’image avec son carré) :

Comme nous pouvons le voir sur le tableau suivant, la lisibilité de l’auto corrélation ou de l’inter corrélation dépend du nombre d’images considérées, et de la lisibilité des tavelures sur ces images (ici l’étoile STF2909) :

Nous pouvons améliorer le rapport signal sur bruit dans la fonction d’auto corrélation en additionnant les transformées de Fourier (c’est ce qu a été fait par A. et S. Rondi). Il suffit pour cela de changer la structure des commandes du premier tableau en :

Mais nous pouvons tout à fait faire la même chose (addition des intercorrélations individuelles) en ce qui concerne la crosscorrélation de l’image et de son carré, et nous constatons immédiatement une amélioration de la lisibilité de la position et de l’angle du couple. On voit tout de suite apparaître la différence d’intensité à droite et à gauche du pic central (différence due aux écarts de magnitude entre les deux composantes du couple). Cette différence, qui est en fait le pourcentage « a » de magnitude de l’étoile la plus faible, normalisée à la composante de magnitude la plus forte (à un coefficient de proportionnalité près dû à l’addition normalisée, mais nous en discuteront plus loin), permet de lever l’ambiguïté de position des composantes. La composante la plus brillante et la moins brillante sont inversées sur l’image d’intercorrélation, par rapport à l’image brute. La procédure pour obtenir cette somme des intercorrélations passe par l’écriture d’un script sous Iris, qui permet de lancer automatiquement le traitement complet d’une séquence. L’après midi du 01/07/08 a été consacrée à l’écriture automatique d’un script pour Iris, en partant d’un tableur Exell (pas très élégant mais efficace au premier abord.). Le fichier Exell permet de répéter les commandes du Tableau 2 600 fois de suite, en changeant le nom du fichier, le coefficient de normalisation du produit et le coefficient de normalisation de la fonction fcorrel. La sauvegarde doit ensuite se faire en format *.txt, codage Unicode. Ce fichier texte est ensuite ré ouvert avec le bloc note, et sauvegardé avec l’extension .pgm (crosscorrel.pgm par exemple), codage ANSI. Sous Iris, dans une fenêtre de commande en ligne, il suffit ensuite de taper la commande run crosscorrel.pgm, et le calcul d’intercorrélation des 600 images de la séquence est lancé. L’inconvénient de cette méthode est sont temps de calcul. En effet, il faut au moins 30 minutes avec un Pentium 1.86GHz disposant de 1Go de mémoire vive pour faire la cross corrélation de 600 images avec leurs carrés respectifs. L’ensemble des résultats, tant sur la mesure de l’écartement que sur les angles de positions semblent être plus faciles à déduire des images de sommes d’intercorrélations. Les images suivantes présentent les sommes de 600 images des autocorrélations et intercorrélations obtenues lors de la première nuit d’observation de cette mission. Le but de cette première session était de vérifier la précision de la méthode en terme d’écartement. Nous n’avons procédé à un étalonnage angulaire que lors de la deuxième nuit d’acquisition. La mesure de l’écartement se fait par un simple relevé de la position du maximum du pic correspondant a l’une ou l’autre des 2 étoiles. La différence en deltax et deltay par rapport au point central de l’image d’intercorrélation permet de remonter à l’écartement : rho(pixels)=racine ((deltax)²+(deltay)²) La conversion en seconde d’arc dépend de l’échantillonnage. Soit nous pouvons utiliser une mesure absolue en faisant confiance au calcul théorique, ce qui est risqué, car l’incertitude dépend fortement d’un paramètre difficile à mesurer : le tirage de la bague allonge. Soit nous utilisons une étoile étalon dont une mesure récente nous renseigne sur l’échantillonnage de notre image. Les résultats présentés en suivant sont établis en partant du calcul théorique sur l’échantillonnage. Nous verrons au cours de la deuxième session comment obtenir un étalonnage correct. Les intercorrélations présentées ci-dessous ont toutes été réalisées avec un tirage de la bague allonge maximum, à l’exception de Mu Cyg (STF2822) pour laquelle le montage a été réduit de 4mm au cours des manipulations. Nous verrons sur les mesures que l’on reste cohérent aux mesure récentes tirées des circulaires officielles de l’UAI concernant la mesure de certains couples (les circulaires UAI citées sont celles que l’on peut trouver notamment sur le site de l’USNO, et dont le lien se trouve plus bas).

Premier constat plutôt rassurant : Véga est une étoile simple !!! 😉 Qu’en est-il des autres étoiles observées :
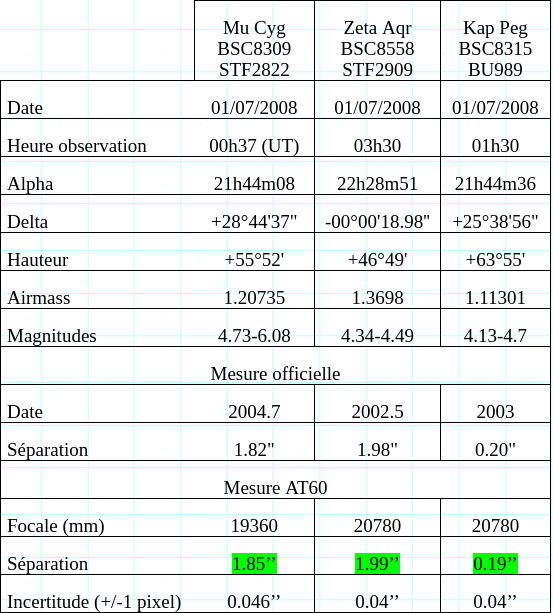
On n’est pas du tout en dehors des clous, bien au contraire !! L’incertitude associée, est due à la lecture de la position du pixel mesuré dans l’intercorrélation. Dans les trois cas, on retrouve une mesure approchant la valeur officielle la plus récente que nous ayons pu trouver dans la littérature. Nous avons, certes, été un peu optimiste en ce qui concerne BU989. L’échantillonnage étant de l’ordre du dixième de seconde par pixel, une étoile double à 0.19’’ est à 2 pixel du centre de l’image d’intercorrélations (voir traits rouges sur le cliché.). Autrement dit, on atteint les limites. Mais les deux excroissances que l’on peut noter sont significatives par rapport à l’intercorrélation que nous avons obtenue sur une étoile simple comme Véga. De plus on constate avec joie que l’intercorrélation nous permet de lever l’ambiguïté sur la position de l’étoile la plus brillante du couple. Sur STF2822, l’intensité de l’intercorrélation est plus importante sur le pic du haut que sur le pic du bas. Ce qui signifie que l’étoile la plus brillante du couple est celle du bas. De la même manière, pour STF2909, l’étoile la plus brillante est celle située à gauche du couple. Les résultats ne sont donc pas décevants, bien au contraire…..
Nuit du 03/07 au 04/07/2008 : Mesure complète sur une étoile double
Ayant constaté la nuit précédente que l’on fait les choses correctement, nous avons affiné la méthode de manière à pouvoir effectuer une vraie mesure complète effectivement exploitable. La première étape pour mesurer une étoile double consiste à étalonner le système sur 2 paramètres : L’échantillonnage et l’angle de la caméra par rapport au Nord. La calibration peut se faire de deux manières : soit utiliser un couple étalon de faible déplacement angulaire et d’écartement faiblement variable, soit procéder (Pour l’écartement) à une mesure fine de l’échantillonnage en utilisant un masque de Fizeau (il en existe un dans la labo du T60). Un masque de Fizeau est un cache en carton se fixant devant le télescope, et disposant de 2 ouvertures. On obtient, une image de franges d’interférences, dont l’écartement est directement lié à l’échantillonnage de l’ensemble optique. Le masque de Hartmann actuellement utilisé pour la mise au point pourrait faire l’affaire. Nous ne l’avons pas utilisé, mais lors d’une prochaine mission, il semblerait intéressant de faire un essai avec. Dans tous les cas, pour ce qui est de l’orientation caméra, il faut en passer par un couple étalon. La méthode du filé d’étoile est peu précise dans notre cas, car la forme de la tache de diffraction est tellement empâtée, qu’il est difficile de procéder à la mesure des centroïdes. Nous avons choisi pour cette nuit, d’utiliser l’une des étoiles doubles Epsilon Lyre. Un peu au hasard (nous avions le choix entre 2 étoiles), nous avons pointé Epsilon2 Lyre :

L’orientation et le tirage de la caméra à été figée une fois pour toutes afin de mesurer l’étoile cible. Nous verrons plus bas le résultat de la mesure de l’intercorrélation sur la mesure de notre étoile de calibration. La cible que nous avons choisie est une étoile de séparation angulaire inférieure à la barre mythique de 1’’ d’arc. Il s’agit de l’étoile Zéta Bouvier, dont la séparation est prévue à 0.6’’ environ. Voici le résultat de l’acquisition :

L’étoile apparaît complètement empâtée, il semble impossible de mesurer quoique ce soit sur les images individuelles. On constate, malgré tout, une similitude entre la structure fine des tavelures et la simulation obtenue sous Abberator. Si nous procédons comme précédemment, nous obtenons les fonctions d’autocorrélations et d’intercorrélations suivantes :

A part la mise en évidence d’une légère défocalisation sur Espilon2 lyre, les intercorrélations obtenues pour les 2 étoiles sont parfaitement lisibles. Quels sont les paramètres de cette observation :
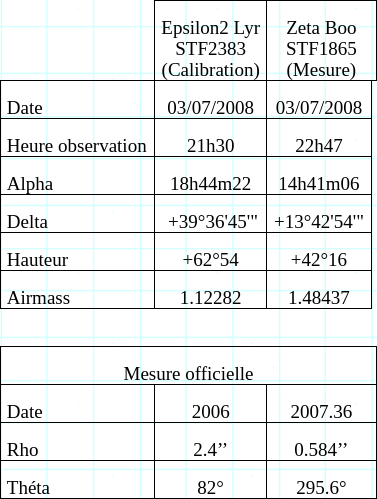
Pour matérialiser complètement la mesure, nous superposons les intercorrélations respectives des 2 étoiles (calibration et mesure) :

La mesure de Rho se fait comme précédemment. La mesure de Théta nécessite quand à elle d’avoir la position du méridien sur l’image. L’angle de position de l’étoile étalon est de 82°. On rappelle que l’angle de position est compté positivement dans le sens trigonométrique (sens inverse des aiguilles d’une montre), partant du nord. Dans le tableau n°6, il s’agit de l’angle b. L’angle de position de l’étoile mesuré est lui dépendant de l’étoile prise pour origine. La levée d’ambiguïté peut être réalisée si l’écart de magnitude est suffisant sur l’image d’intercorrélations. Ce n’est malheureusement pas le cas pour Zeta Boo. L’angle de position pour cette étoile est donc soit de b+d+180, soit de b+d. La seule indication que nous avons est la mesure faite sur Zeta Boo en 2008 (USNO) qui nous donne un angle de 295.6°.
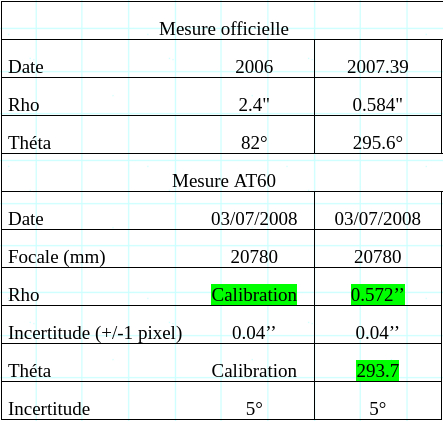
Le résultat est particulièrement probant. En effet, compte tenu de l’incertitude sur la valeur de Rho (4 centième de secondes), nous sommes à 0.01’’ de la mesure la plus récente (INFORMATION CIRCULAR No. 163 (OCTOBER 2007) INTERNATIONAL ASTRONOMICAL UNION COMMISSION 26 (DOUBLE STARS)). Pour la mesure de l’angle de position, l’incertitude croit avec Rho décroissant autrement dit, plus l’étoile est serrée, plus l’incertitude sur Théta est importante. A 0.5’’, nous sommes ici à +/-5°. La valeur mesurée est tout de même cohérente (2° d’écart à la mesure la plus récente) Compte tenu des nombreux objectifs de la mission, nous nous sommes arrêté là pour la partie interférométrie.
Conclusion
En conclusion de cette partie, on peut tout de même dire quelques mots : Le T60 est parfaitement adapté à ce genre de mesures. A titre de comparaison, on peut noter que le programme de recherche américain de l’US Naval Observatory utilise un télescope de 66cm de diamètre en interférométrie des tavelures pour établir depuis 1992 (http://adsabs.harvard.edu/abs?bibcode=1997ApJS..111..289D&😉 le ”Fourth Catalog of Interferometric Measurements of Binary Stars Alors pourquoi ne pas envisager de faire un véritable programme de mesure d’étoiles doubles par interférométrie des tavelures au T60 ? La méthode est simple, le protocole connu (étalonnage de l’échantillonnage et de la position angulaire), et la puissance des logiciels de traitement d’images amateurs sont parfaitement adaptés à ce genre de travail. En dernier lieu, voici une petite bibliographie utile pour se mettre un peu d’interférométrie en tête….
Bibliographie
Pages de A. et S. Rondi => Les fondamentaux : http://astrosurf.com/rondi/Speckle.htm
Les premiers essais au T60, par A. et S. Rondi : http://www.astrosurf.com/rondi/t60/crabe-tambour/speckle.htm
La méthode d’auto corrélation et d’inter corrélation : http://www.astrosurf.com/rondi/binary_cross-correl.htm
Programme de recherche sur les étoiles doubles à l’USNO : https://www.usno.navy.mil/USNO/astrometry/optical-IR-prod/wds
Base des étoiles doubles de l’observatoire de Nice (Sidonie) : http://sidonie.obs-nice.fr/scripts/SidonieAccueilF.asp
Catalogue USNO d’étoiles doubles résolues en Interférométrie des tavelures : https://www.usno.navy.mil/USNO/astrometry/optical-IR-prod/wds/int4