Sommaire
Mission T60 (Speckles Pic II) du mois de Novembre 2008 (17/11/2008 au 24/11/2008)

Introduction :
Lors de notre précédente mission (http://www.astrosurf.com/t60/missions/compte_rendu_mission_Speckles_pic_I_MCA.pdf), nous avons montré qu’il était possible, avec une manip simple, d’utiliser la méthode de l’interférométrie des tavelures (Speckle interferometry) pour étudier des étoiles doubles serrées. Quand nous parlons d’étoiles doubles serrées, il faut rappeler que la séparation théorique donnée par un télescope dépend dans un premier temps de la diffraction par l’ouverture circulaire du télescope, et dans un deuxième temps par la qualité de la turbulence.
La turbulence agissant de manière complètement aléatoire, la somme des poses individuelles d’une séquence vidéo ne permet pas par simple « Shift and add » de remonter aux informations de position du couple considéré avec une précision importante (de l’ordre de quelque dizaines de milli arc secondes (mas). La méthode employée lors de notre mission précédente (somme des cross corrélations de chaque images sur une séquence de 600 à 1800 images), permet d’extraire du bruit atmosphérique la donnée de séparation et d’angle au nord d’un couple d’étoiles serrées.
L’objet de notre mission était donc d’effectuer un certain nombre de mesures sur une liste d’étoiles de séparation inférieure à 2’’5 et ayant un différentiel de magnitude inférieur à 3. Nous avons procédé à l’acquisition des séquences vidéos à l’aide des éléments que nous avions montés là haut lors de la première mission (bague allonge Meade, bague monture C pour la Watec 902H2, et bague adaptation sur le nouveau porte oculaire récemment mis en place sur le T60 La caméra est suivie d’un numériseur Pinnacle Dazzle video recorder, du même type que celui utilisé pour la manip d’occultation d’étoiles au T60. Les vidéos acquises sont des AVI enregistrés sous Virtualdub en mode Raw. La cadence est de 25 ips, le temps de pose annoncé par le datasheet de la caméra est de 20ms.
Pour donner un peu en avance le rendement de la mission, le pointage, avec un peu d’habitude, prend moins de 5 minutes par étoiles, et l’acquisition environ 2 minutes. La moisson totale d’étoile (44 étoiles au total de cette mission) s’est faite dans le temps record d’une nuit et demi environ. Compte tenu de la météo plutôt défavorable que nous avons eu en deuxième partie de mission, nous avons tapé dans le mille.
Pour ce qui est du choix des cibles, quelques discussions et recherches sur Internet m’ont convaincu de m’attaquer, pour commencer, à une liste bien connue des duplicistes, la liste « Morlet-Durand » établie en Avril 2002 par la SAF (Société Astronomique de France) contenant 387 étoiles de référence : (http://saf.etoilesdoubles.free.fr/documents/387_DOUBLES.pdf), extraites du Washington Double star catalogue. Patrick Lailly, que nous avons cité dans notre compte rendu précédent, en a extrait une liste secondaire pouvant servir de base à une manip interférométrie des tavelures (commencée au Télescope Jean Marc Salomon de Planète Science : http://pagesperso-orange.fr/patrick.lailly/astro/tavelures/manips/select_double.html) Nous nous sommes basés sur cette extraction pour commencer notre programme d’observation d’étoiles doubles. Les étoiles de la liste que nous n’avons pas put imager sont celle dont l’ascension droite les rendait inaccessibles à l’observation à cette période. On peut donc estimer que le rendement moyen à l’observation est d’environ 30 étoiles par nuit, à raison d’environ 7 minutes par étoiles.
Choix de méthode de calibration :
Premier gros problème, l’étalonnage des mesures. Le calcul de l’échantillonnage découle du schéma optique d’un système à tirage oculaire classique suivant :
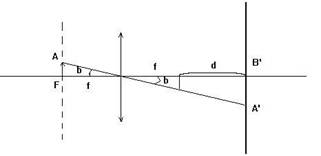
En appelant FA la taille de l’image de l’objet observé au foyer du miroir primaire, nous pouvons écrire FA=F.tg(alpha) avec alpha l’angle sous lequel est vu l’objet. Cet angle étant petit, on considère tg(alpha)=alpha. Il vient alors pour l’échantillonnage la relation suivante :
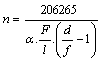
en secondes par pixels (alpha exprimé en secondes). Avec F la focale de l’objectif connue à +/-5mm, f celle de l’oculaire, d le tirage (connu à +/-0.5mm) et l la taille du pixel. L’échantillonnage théorique est alors voisin de 0.086’’/pixels. Mais nous devons aller plus loin pour définir une valeur précise. Nous avons essayé d’utiliser la technique du masque de Fizeau (nous l’avions envisagé lors de la première mission). Le masque présent au T60, utilisé à l’origine pour la mise au point précise, dispose de 3 trous (masque de Hartmann). Nous en avons obturé un et utilisé les 2 autres, en notant leurs caractéristiques (écartement B=285mm, et taille des ouvertures S=160mm). L’étoile utilisée pour faire le test était Gamma Pégase (BSC39 ‘Algenib’, Alpha = 00h13m14.200s | delta = +15°11’01.00 » le 17/11/2008 à 21h30. Hauteur = 61°17’, Airmass =1.13). Nous en avons d’ailleurs profité pour vérifier la présence des tavelures avant l’apposition du masque :
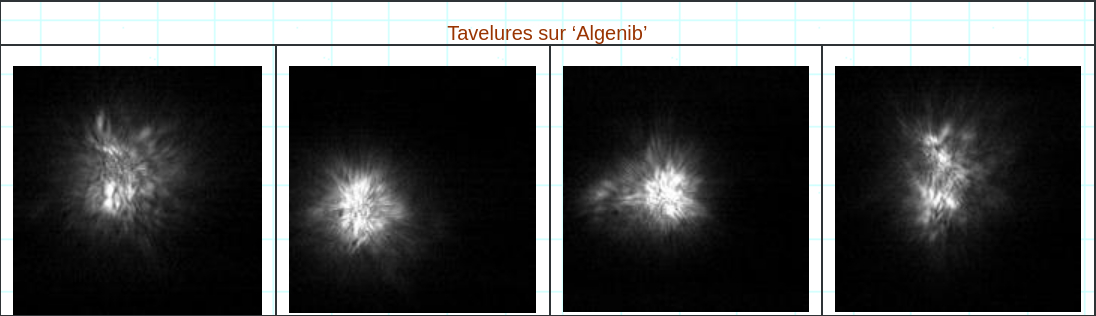

Les franges d’interférences sont bien présentes sur la séquence vidéo. L’extraction de la périodicité des franges s’est faite par recherche du maximum de la FFT dans la fenêtre correspondant au pic de franges. Par la méthode du masque de Fizeau, un problème fondamental se pose : la formule du tirage oculaire définie ci-dessous implique une parfaite connaissance de la longueur d’onde :
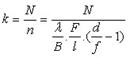
avec N la taille de l’image de la FFT, B l’écartement des trous, F la focale de l’objectif, f celle de l’oculaire, d le tirage et l la taille du pixel. Nous pouvons faire une estimation du maximum de sensibilité spectrale du capteur, mais la précision reste insuffisante pour avoir une mesure fiable de l’échantillonnage (il suffit de constater la dispersion des points correspondants à la périodicité des franges). Le terme en lambda/B introduit une imprécision due au fait que la mesure présentée ici n’est pas spectralement filtrée. Malgré tout nous avons une mesure dont l’ordre de grandeur est cohérent si la longueur d’onde du maximum de sensibilité de la caméra est voisine de 0.61 microns :

Mieux vaut donc en rester à une procédure de calibration plus « classique » pour mesurer les couples considérés. Nous avons choisi comme couple étalon, STF958 pour établir la calibration en rho et en théta. Conformément aux préconisations du livre de Paul Couteau, nous avons utilisé une étoile qui au moment de l’observation se trouvait le plus haut possible, afin d’éviter la perturbation induite par la réfraction atmosphérique. La caméra ayant été immobilisée pendant toute la durée des acquisitions (2 nuits), l’étoile de calibration été imagée à la fin de la première nuit. Les calculs de la valeur de la hauteur et de la couche d’air traversée (airmass) ont été établis à l’aide du logiciel Prism V6 :


La position des centroïdes des étoiles est obtenue par l’algorithme de recherche par la méthode d’ajustement d’une gaussienne 2D sur l’étoile (Prism V6). Dans la suite de ce document, c’est cette méthode qui a été principalement utilisée. Toutefois, dans certains cas d’images de speckles ou l’algorithme ne convergeait pas, la détermination de position s’est faite à l’aide de la routine de calcul du barycentre des pixels dans une fenêtre ajustée au pic de corrélation considéré. L’angle Béta n’est pas l’angle de position du couple, mais l’angle du couple à l’axe x de la caméra.

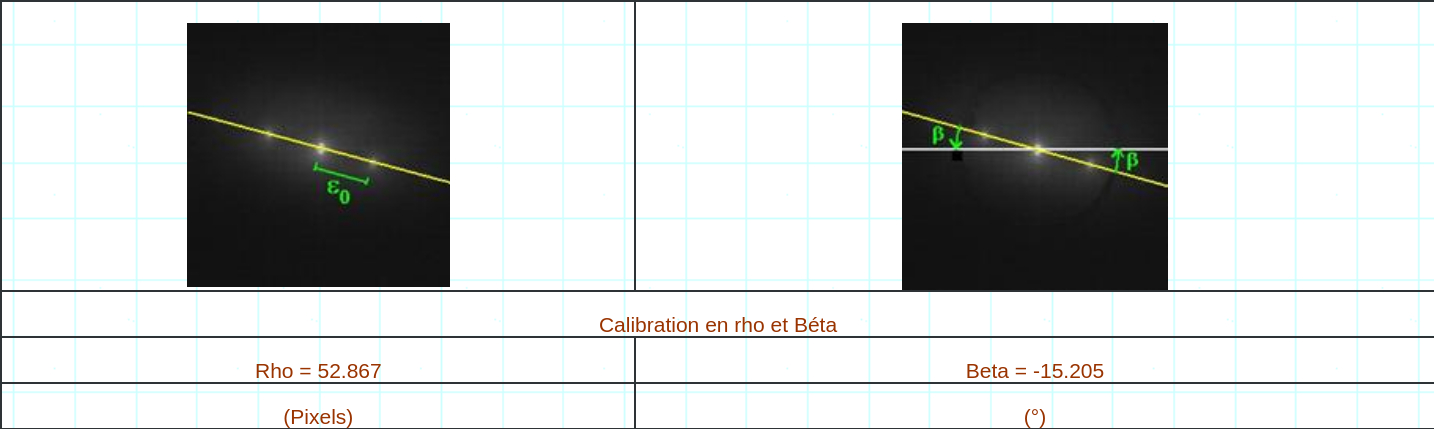
Pour établir les valeurs de références de epsilon et de théta, nous avons maintenant besoins des mesures officielles récentes de notre étoile étalon. Nous avons utilisé pour cela le ”Fourth Catalog of Interferometric Measurements of Binary Stars” (https://www.usno.navy.mil/USNO/astrometry/optical-IR-prod/wds/int4), dont nous avons extrait les données relatives a l’étoile STF958 :

La dernière mesure disponible sur ce catalogue est donc relativement ancienne puisqu’elle date de fin 2002. Nous avons donc comme indication Rho = 4.55 et Théta = 256.3. A en croire les informations relatives à l’angle thêta, issu du wds ce dernier est stable depuis plusieurs années. Nous considéreront la valeur 256.3° comme référence. La magnitude respective des 2 composantes nous pose un problème quand à la position du nord sur l’image. En effet, la mesure de thêta se fait dans le sens direct (aussi appelé trigonométrique ou encore inverse des aiguilles d’une montre) en partant de l’axe au nord. Dans le cas qui nous intéresse, nous avons 2 solutions pour orienter nos clichés à 180° près. La levée d’ambiguïté se fait par l’utilisation d’une deuxième mesure sur une étoile multiple (nous avons ici utilisé la mesure de STF948), dont nous présentons ci-dessous les mesures officielles du ”Fourth Catalog of Interferometric Measurements of Binary » :


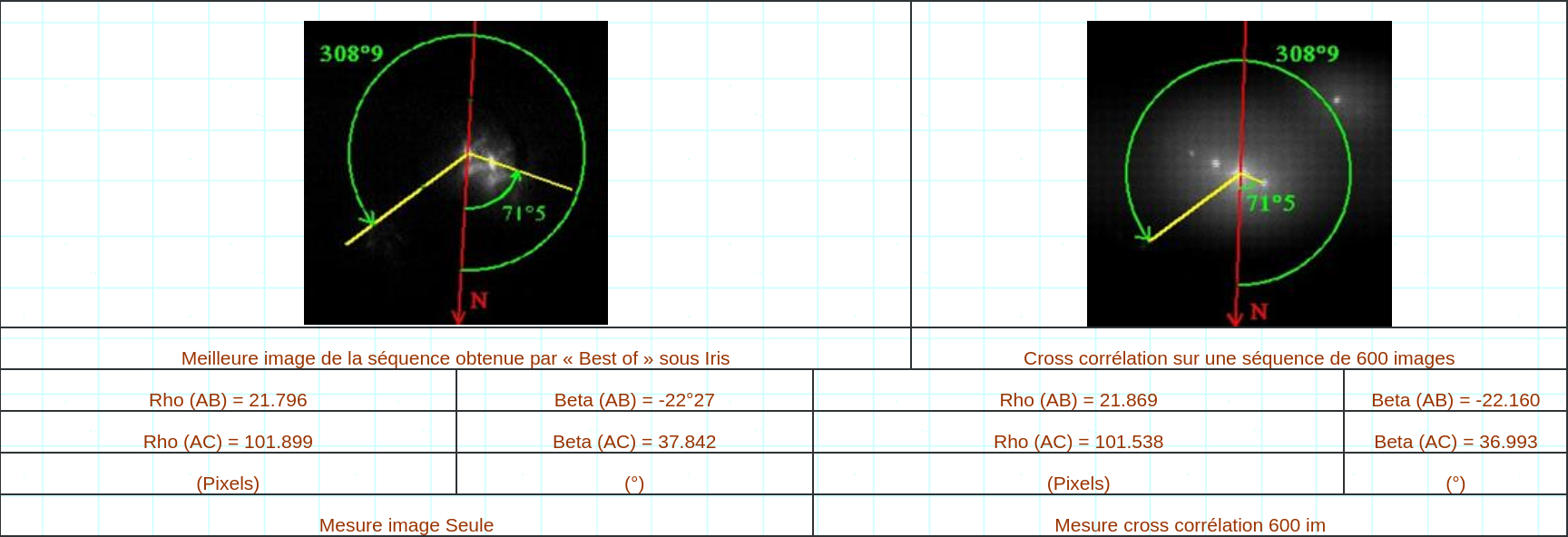
Nous savons donc maintenant que l’axe nord est situé vers le bas, ce qui nous permet d’établir la relation algébrique de mesure des angles :
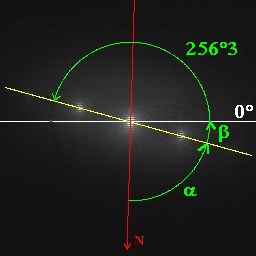
La mesure de l’angle de position se faisant par rapport à l’horizontale à l’aide de la relation :
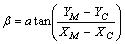
avec Xc et Yc les coordonnées du centre de l’image Nous en déduisons la mesure de l’angle entre l’horizontale et l’axe Nord :

Avec bêta l’angle à l’horizontale, thêta l’angle de position de l’étoile se déduit de la relation algébrique :
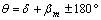
Le terme en +/- 180° est issu du choix de l’étoile d’origine. Nous avons pris comme valeur étalon l’intermédiaire entre la mesure directe et la mesure par corrélation :
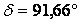
Pour la mesure de l’écartement, la cohérence des mesures entre STF948AB et STF948AC et STF958AB est problématique. En effet, la mesure de STF958 en 2002 donne une valeur de 4’’55 ce qui nous donne un échantillonnage de 0.0864’’/pixels par mesure directe (image brute et shift and add), et de 0.0860’’/pixels par cross corrélation. Si nous appliquons ce résultat à STF948AB et AC, nous obtenons unes séparation pour AB de 1’’872 et pour AC de 8’’753. Si nous comparons ce résultat aux mesures du ”Fourth Catalog of Interferometric Measurements of Binary » , la séparation des composantes AB et AC semble surévalué dans les 2 cas, surtout pour ce qui est de la valeur de la séparation de STF948AC. La séparation de ce couple, sur une quinzaine d’année (1991-2006), varie autour d’une valeur moyenne de 8.678’’ avec un écart type de 0.038. Nous sommes donc entre 2 et 3 fois l’écart type au dessus la valeur de l’ensemble des mesures récentes faites sur ce couple. La situation est identique sur STF948AB. Nous avons donc considéré l’écartement pour la calibration non pas de STF958AB (vu l’ancienneté de la mesure), mais bien celui de STF948AC, qui de plus au vue de son écartement plus important, nous donne une précision meilleure pour la mesure de notre échantillonnage. Nous obtenons donc comme valeur de l’échantillonnage :
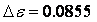
en arcsec/pixels
Cette valeur nous amène à considérer l’ordre de grandeur de l’erreur sur la mesure comme voisine de +/-20mas à 2 sigma.
Les résultats :
Tous les résultats des lesures de cette mission sont disponibles de façon détaillée sur ce lien. Venons en maintenant au rapport des mesures proprement dit. Le tableau suivant récapitule à la fois les mesures directes (lorsque ces dernières se sont avérées possibles) et les mesures effectuées sur les pics de la cross corrélation : Les colonnes Airmass et hauteur correspondent respectivement à l’épaisseur de couche d’air et a la hauteur de l’astre, calculés au moment de l’acquisition de la vidéo, à l’aide du logiciel Prism. Les magnitudes sont extraites du WDS.

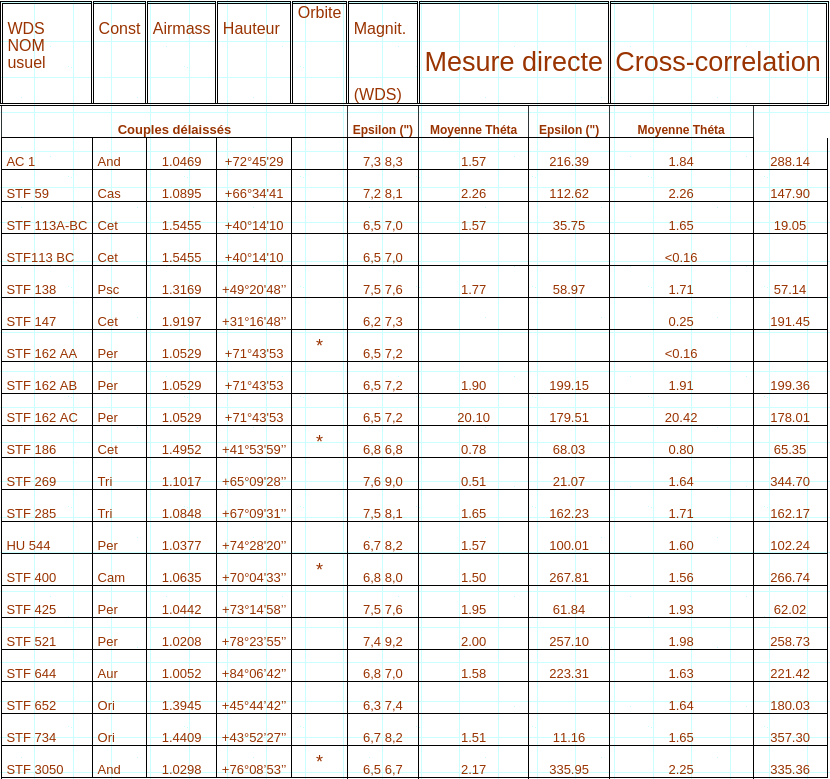
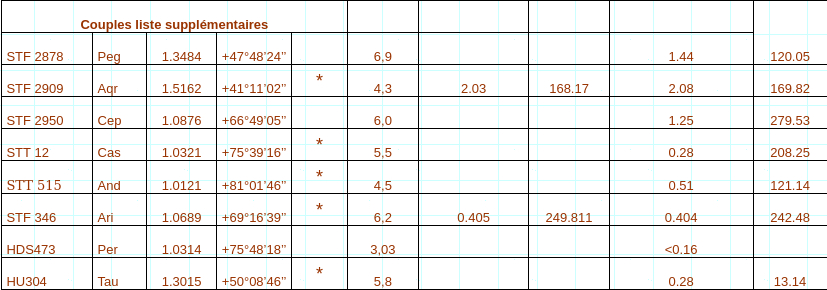
Discussion sur les mesures :
Nous allons présenter ici 3 mesures complètes. Chaque vidéo acquise a fait l’objet d’un certain nombre d’opérations : Dans un premier temps, la vidéo à été convertie à l’aide du logiciel Iris en images format Fits susceptibles d’être utilisées. Une sélection par « bestof » à été opérée afin d’extraire les meilleures images de la séquence. Puis nous avons utilisé sur l’ensemble de la séquence, le générateur de script (fichier exel) que nous avons cité dans le premier compte rendu. Ce fichier permet de générer un script de calcul de la somme des intercorrelation entre l’image et son carré (cross-correlation), exécutable sous Iris (ce fichier est disponible sur demande en m’envoyant un mail à l’adresse (btregon@club-internet.fr). Le résultat de ce calcul sert de base à la lecture des paramètres de position de l’étoile double. Nous présentons ici l’analyse faite sur STF2909AB, que nous avions déjà étudié lors de la mission précédente

L’extraction de Rho et Théta se fait d’abord par mesure directe (quand cela est possible), sur la meilleure image de la séquence. On extrait bêta et par les paramètres de calibration vus plus haut, on remonte à l’écartement et l’angle de position. Nous verrons plus loin que la présence des speckles rend parfois cette opération impossible. Dans un deuxième temps, on procède à l’analyse de l’image de cross corrélation en mesurant la position des 2 pics (correspondant au maximum de cohérence du couple dans la séquence vidéo, nous verrons cela plus bas). Une fois mesurés les 2 pics, nous faisons la moyenne des écartements et des angles de positions.
Afin de comparer la validité des nos mesures avec la littérature, nous avons ensuite procédé sur chaque couple au récapitulatif suivant :
Récupération des mesures disponibles sur le couple via différentes sources (USNO, Observatoire de Nice « Sidonie http://sidonie.obs-nice.fr/scripts/SidonieAccueilF.asp»)
– Récupération des paramètres d’orbites officiellement publiés (même source)
– Simulation et ajout sur le même graphe des mesures obtenuesL’ensemble des simulations ont été réalisées à l’aide du fichier Exel de calcul des orbites, disponible sur le site de A. et S. Rondi : (http://www.astrosurf.com/rondi/t60/crabe-tambour/speckle.htm) Les éléments orbitaux utilisés sont les éléments dynamiques et les éléments de Campbell. :

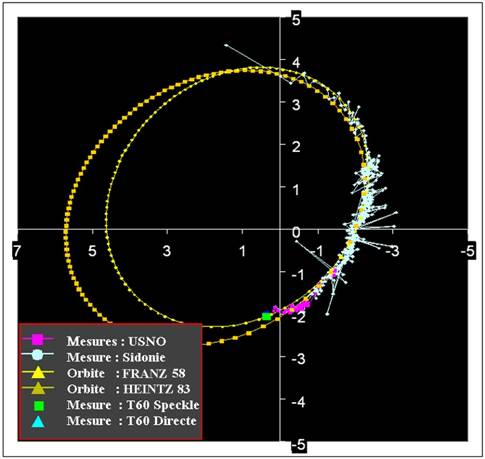
STF2909 (nord en haut)
Tous les couples étudiés ont fait l’objet de ce traitement. Seulement 18 étoiles sur les 44 disposent d’une orbite déterminée. Nous prendrons à titre d’exemple pour illustrer la corrélation avec les mesures officielles le cas de l’étoile STF228 :



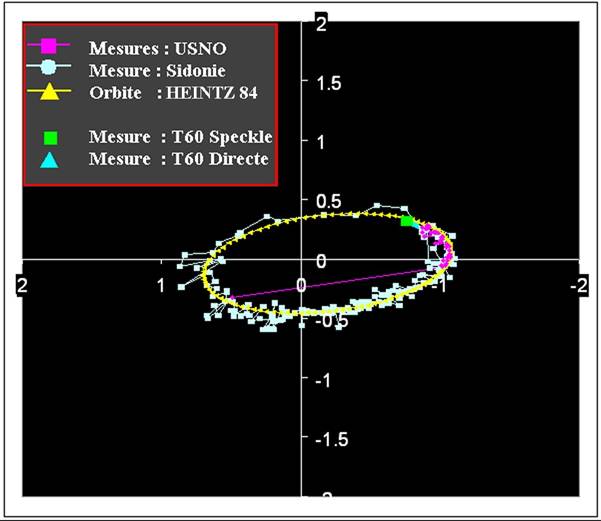
STF228 (nord en haut)
Nous pouvons voir ici que les mesures sont particulièrement bien corrélées avec la liste des mesures officielles. Un premier constat est, par contre, que les pics de cross corrélation sont souvent étalés pour les étoiles dont la séparation est inférieure à une seconde. Cet étalement peut être interprété comme une distorsion locale due à la turbulence durant le temps d’acquisition de la vidéo. Nous discuteront ce point plus loin.
Nous pouvons poursuivre avec l’analyse que l’on peut considérer comme limite, d’une étoile de séparation inférieure à 0.5’’.
Exemple d’un système serré :
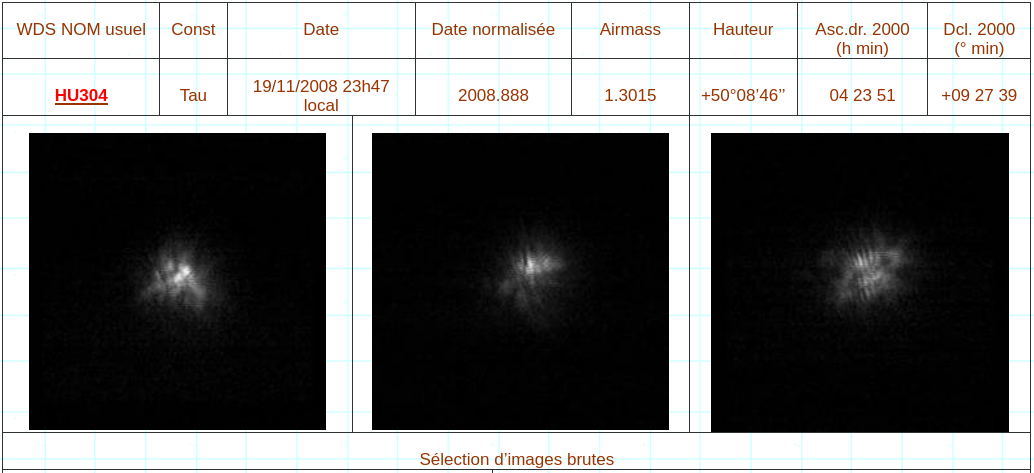

HU304 est un cas limite, l’obtention de la position des pics de maximum de cohérence est obtenue par calcul du centre de gravité des pixels hors axe, dans une fenêtre symétrique de part et d’autre de l’origine, entourant la position estimée du pic de cohérence. L’incertitude est donc très importante sur l’angle thêta.

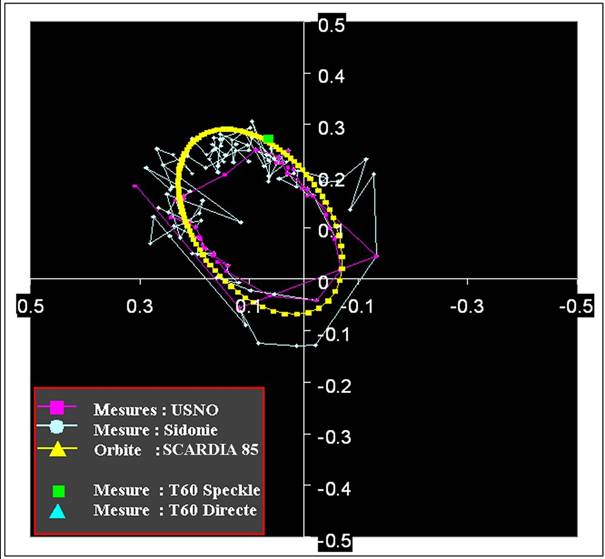
HU304 (nord en haut)
Nous voyons ici que malgré la dispersion (l’étalement) de la cross corrélation, les mesures sont en accord avec les orbites prédites, à la condition toutefois de faire une analyse correcte de la géométrie de l’étalement des pics. Nous verrons cela plus loin.
Discussion sur la méthode d’extraction :
Plusieurs solutions dans l’analyse des pics se présentent : soit une analyse que l’on pourrait qualifier de statistique (qui consiste à considérer que la somme des corrélations nous donne accès à la position réelle du couple, via sa probabilité temporelle d’apparition dans l’image), soit une analyse purement géométrique, consistant à considérer la position du centre des pics, en analysant la dispersion (hors des intensités intrinsèque des pixels du pic de corrélation). N’étant pas encore suffisamment au fait de ces techniques, j’ai intuitivement choisi d’utiliser la première analyse, à savoir la détermination de la position du pic par interpolation avec une fonction gaussienne, et si l’algorithme ne convergeait pas, via la détermination du centre de gravité du pic de corrélation. L’étalement du pic à empêché dans certain cas (pour les étoiles très rapprochées, typiquement moins de 0.2’’), d’établir une mesure sans ambiguïté. Ce fut le cas pour 4 étoiles sur les 44 observées. Dans les cas où le rapport signal sur bruit était insuffisant sur la mesure de la corrélation, il a été nécessaire de travailler sur un nombre plus important d’images (jusqu’à 1800, soit 3 séquences de 600 images). Ceci s’interprète à la fois comme conséquence de la limite sur la magnitude, mais plus particulièrement par une décohérence prononcée due à une forte turbulence atmosphérique locale. Si nous faisons une comparaison brute de la méthode de lecture directe de la position, par rapport à une approche par étude de la corrélation, nous pouvons dégager un avantage certain en faveur de cette dernière méthode. En effet, la totalité des mesures a pût être effectuée par l’analyse de la corrélation, alors que les vidéo comportant un grand nombre de speckles qui n’ont put être dissociées, ont empêché la mesure directe (17 étoiles non mesurées par lecture directe).
Nous pouvons voir sur l’exemple de STF333AB et STF2909 que les speckles rendent impossible la détermination des position des centroïdes des étoiles étudiées :

La cross corrélation permet d’étudier en particulier la présence des similitudes correspondant à l’image du couple hors turbulence, reproduite un certain nombre de fois sur la même image par la distorsion de la turbulence:

Les cercles de couleurs identiques reproduisent l’image unique du couple, que la turbulence, agissant comme un système de déformation optique, reproduit en plusieurs exemplaires. Ce phénomène induit en particulier une incertitude notable sur l’écartement, mais aussi sur les angles que l’on mesure sur un image unique. Prenons le cas de STF 652 pour laquelle la turbulence provoque un phénomène d’interférence locale, rendant impossible une analyse de position cohérente d’une image sur l’autre :
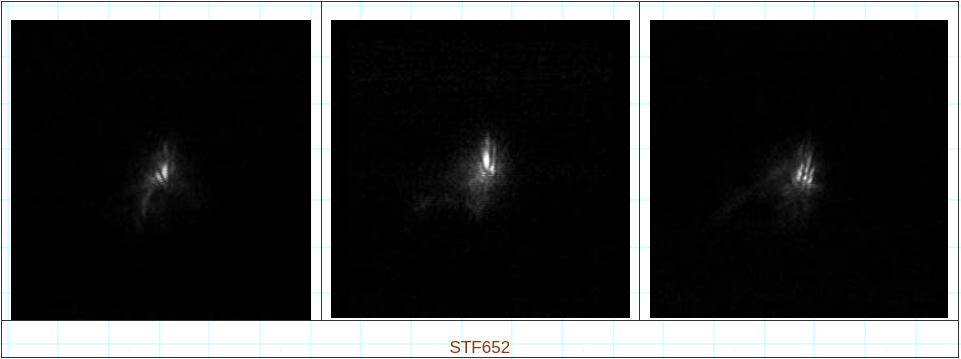
Conclusion :
La météo au cours de cette mission nous a permis de travailler sur un total de 47 étoiles. 3 étoiles de la sélection de départ on été rejetées pour des raisons de hauteur sur l’horizon, qui après examen des positions semblaient hors des conditions de mesures définies dans le livre de Paul Couteau. Au total 44 étoiles se sont avérées vraiment exploitables. Un constat personnel sur la méthode de dépouillement actuellement utilisée : autant l’acquisition est rapide (dans une prochaine mission, avec des conditions de météo favorables, il peut être envisageable facilement de doubler voire tripler le nombre d’étoiles étudiées), autant le traitement actuel est long et fastidieux (près de 2 mois pour compléter le dépouillement). Un autre point à approfondir, est celui de l’utilisation pour la détermination de la position du pic de maximum de corrélation, d’une procédure de type « fit gaussien ». D’autres méthodes seraient peut-être plus adaptées et plus précises pour la mesure de cette position. Au rang des perspectives à envisager, il serait peut-être intéressant de coupler l’analyse interférométrique à une analyse spectrale, afin de compléter l’étude d’une étoile double serrée sur 3 dimensions. Je ne désespère pas avoir un jour le temps de me mettre à la spectro….. Une question que l’on peut aussi se poser est, jusqu’a quel écartement limite peut-on descendre en utilisant cette méthode ? On peut intuitivement penser atteindre le seuil de séparation théorique du T60 (ce qui à 0.55microns de longueurs d’onde est de 0.23 secondes), mais certaines mesures semble montrer que l’ont peut descendre encore au dessous en augmentant l’échantillonnage. Une mission ultérieure nous le dira peut être.